Wieso wird vor dem Integral ein Minus geschrieben?

Question

Aufgabe:

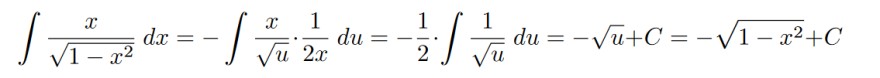
Text erkannt:

\( \int \frac{x}{\sqrt{1-x^{2}}} d x=-\int \frac{x}{\sqrt{u}} \cdot \frac{1}{2 x} d u=-\frac{1}{2} \cdot \int \frac{1}{\sqrt{u}} d u=-\sqrt{u}+C=-\sqrt{1-x^{2}}+C \)

Problem/Ansatz:

Wieso wird vor dem Integral ein Minus geschrieben?

Comments

Naja du substituierst mit u= 1/(Wurzel 1-x^2) aber wenn du das ableitest kommt nach den Regeln ein Minus vor die Ableitung

Answer 1

\( \int \frac{x}{\sqrt{1-x^{2}}} \cdot d x \)
Substitution: \( 1-x^{2}=u \rightarrow \sqrt{1-x^{2}}=\sqrt{u} \)
\( \begin{array}{l} x^{2}=1-u \rightarrow \\ x=\sqrt{1-u} \rightarrow \\ d x=-\frac{1}{2 \sqrt{1-u}} \cdot d u \\ d x=-\frac{1}{2 \sqrt{1-\left(1-x^{2}\right)}} \cdot d u \\ d x=-\frac{1}{2 \sqrt{x^{2}}} \cdot d u=-\frac{1}{2 x} \\ \int \frac{x}{\sqrt{1-x^{2}}} \cdot d x=-\int \frac{x}{\sqrt{u} \cdot 2 x} \cdot d u=-\frac{1}{2} \cdot \int \frac{d u}{\sqrt{u}} \end{array} \)