Bestimmen Sie die Nachfragemenge x und den Preis p , für den die Preiselastizität der Nachfrage den Wert -1 besitzt, …

Question

Aufgabe:

Text erkannt:

1. Bestimmen Sie die Nachfragemenge $x$ und den Preis $p$, für den die Preiselastizität der Nachfrage den Wert $-1$ besitzt, wenn die Nachfragefunktion $x(p)=-1 / 8 p+450$ zugrunde gelegt wird.

Problem/Ansatz:

Wie löst man die Aufgabe?
Habe für den Preis 225 und die Menge 422 raus?

Comments

Wie kann man gleichzeitig fragen wie man die Aufgabe löst, und bereits das eigene Ergebnis bekannt geben?

---

Guter Punkt, jedoch ist mein Lösungsweg und Ergebnis ggf. nicht richtig.

---

Wenn Du Deinen Lösungsweg mitteilst, wird Dir jemand sagen können wo allenfalls Fehler sind.

---

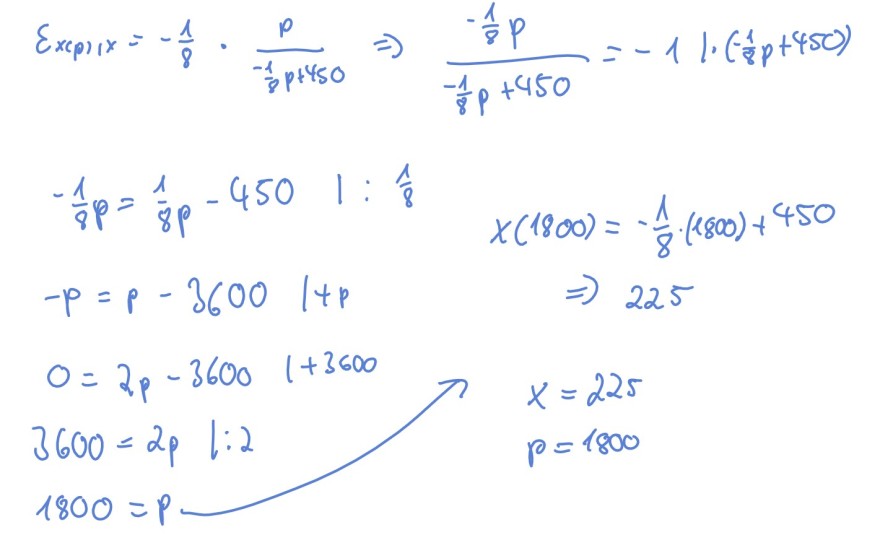
Text erkannt:

$\varepsilon_{x(p), 1 x}=-\frac{1}{8} \cdot \frac{p}{-\frac{1}{8} p+450} \Rightarrow \frac{-\frac{1}{8} p}{-\frac{1}{8} p+450}=-11 \cdot\left(-\frac{1}{8 p} p+450\right)$
$-\frac{1}{8 p}=\frac{1}{8 p}-450 \quad 1: \frac{1}{8}$
$-p=p-3600 \quad 1+p$
$\begin{aligned} 0 &=2 p(1800)=-\frac{1}{8} \cdot(1800)+450 \\ & \Rightarrow 225 \end{aligned}$
$3600=2 p+1: 2$
$1800=p$
$x=225$
$p=1800$

Habe doch nochmal neu gerechnet, hoffe das ist jetzt richtig ^^

Der Preis, bei dem die Elastizität der Nachfrage = -1 beträgt wäre dann 1800, und die Menge die Nachgefragt wird 225?

Answer 1

Überprüfe mal deine Ableitung.

Wenn du beide Seiten der Gleichung mit -8 multipliziert hättest, anstatt durch 1/8 zu dividieren, wäre es einfacher gewesen und du wärst schneller zum Ziel gekommen.