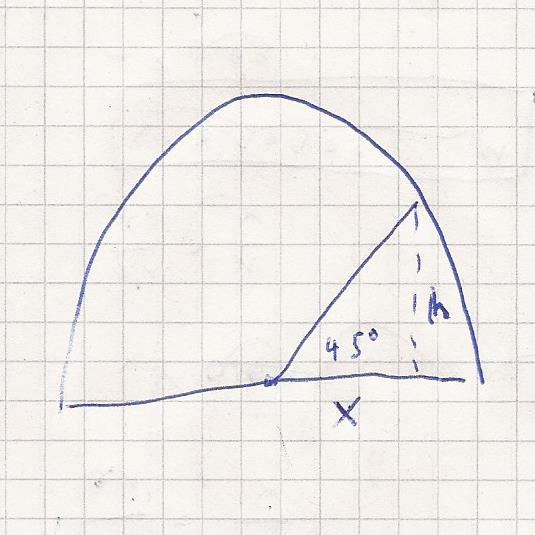Eine Bogenbrücke ist 80 Meter lang und hat einen parabelförmigen Trägerbogen, der in der mitte 8 Meter hoch ist.
A) stellen sie die funktionsgleichung auf, die den Verlauf des Trägerbogens beschreibt, wenn der Ursprung des Koordinatensystems auf Straßenniveau in der Mitte der Brücke liegt.
Parabel
f ( x ) = a*x^2 + b*x + c
Der Scheitelpunkt ( Hocpunkt ist mittig )
f ( x ) = a*x^2 + c
c ist der y-Achsenabschnitt und beträgt 8 m
f ( x ) = a*x^2 + 8
Rechter Auflagepunkt bei
( x | y )
( 40 | 0 )
f ( 40 ) = a * 40^2 + 8 = 0
a = - 0.005
f ( x ) = - 0.005 * x^2 + 8
B) eine zusätzliche metallstrebe soll vom Mittelpunkt der Brücke auf Straßenniveau in einem 45 Grad Celcius Winkel bis zum Trägerbalken verlaufen. In welcher Höhe trifft sie auf den Parabelbogen? Hinweis: Die Steigung der Strebe bzw. Gerade beträgt 1.
tan ( 45 ) = h / x
h := - 0.005 * x^2 + 8
tan ( 45 ) = ( - 0.005 * x^2 + 8 ) / x
1 = ( - 0.005 * x^2 + 8 ) / x
x = -0.005*x^2 + 8
0.005 * x^2 + x = 8
Mitternachtsformel, pq-Formel oder quadr.
Ergänzung
x = 7,7 m
h = -0.005 * x^2 + 8 = - 0.005 * 7.7^2 + 8 = 7,7
x = h
x / h = 1 => a = tan(45) = 1
Bei Bedarf wieder melden.