Variante Döschwo:
C(-200 | -20), D(200 | -20), S(0 | 40)
Gleichungssystem:
\( -20 = a \cdot (-200)^{2} + b\cdot(-200) + c \)
\( -20 = a \cdot 200^{2} + b \cdot 200 + c \)
\( 40 = a \cdot 0^{2} + b \cdot 0 + c \)
Lösung:
a = -3/2000, b = 0, c = 40
Funktion:
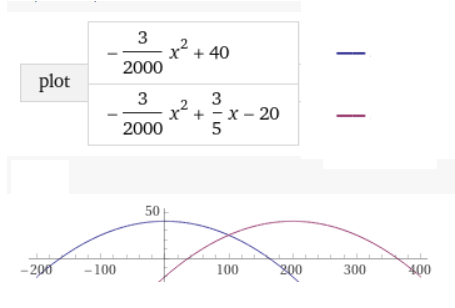
y = \(-\large\frac{3}{2000}\normalsize\) x2 + 40
Variante Moliets:
C(0 | -20), D(400 | -20), S(200 | 40)
Gleichungssystem:
\( -20 = a \cdot 0^{2} + b\cdot 0 + c \)
\( -20 = a \cdot 400^{2} + b \cdot 400 + c \)
\( 40 = a \cdot 200^{2} + b \cdot 200 + c \)
Lösung:
a = -3/2000, b = 3/5, c = -20
Funktion:
y = \(-\large\frac{3}{2000}\normalsize\) x2 + \(\large\frac{3}{5}\normalsize\) x - 20