Ermitteln sie anhand der Zeichnung die Funktionsgleichung

Question

Aufgabe:

Ermitteln sie die Funktionsgleichung der hier dargestellten Funktionen auf dem Bild (Nur Nummer 3 ist mir nicht klar) https://www.mathelounge.de/528847/funktionsgleichungen-zu-den-gezeichneten-graphen
Problem/Ansatz:

Da der Thread schon sehr alt ist, mache ich vorsichtshalber einen neuen auf. Die im vorherigen Beitrag geleisteten Beiträge haben mir nicht weitergeholfen, da a) 2 oder 3 verschiedene Gleichungen angegeben wurden und b nur mit Hilfe der Umkehrfunktion deutlicher auf die Lösung eingegangen wurde, die möchte ich aber wenn möglich weglassen, da es bei den vorherigen Aufgaben auch ohne geklappt hat ( also müsste es ja auch hier einen Lösungsweg ohne Umkehrfunktion geben). Wolfram Alpha scheint mit den beiden Lösungen der Community mir auch keinen gescheiten Graphen anzeigen zu können (siehe Bild, der Graph verläuft nicht weiter ab einem bestimmten Definitionsbereich)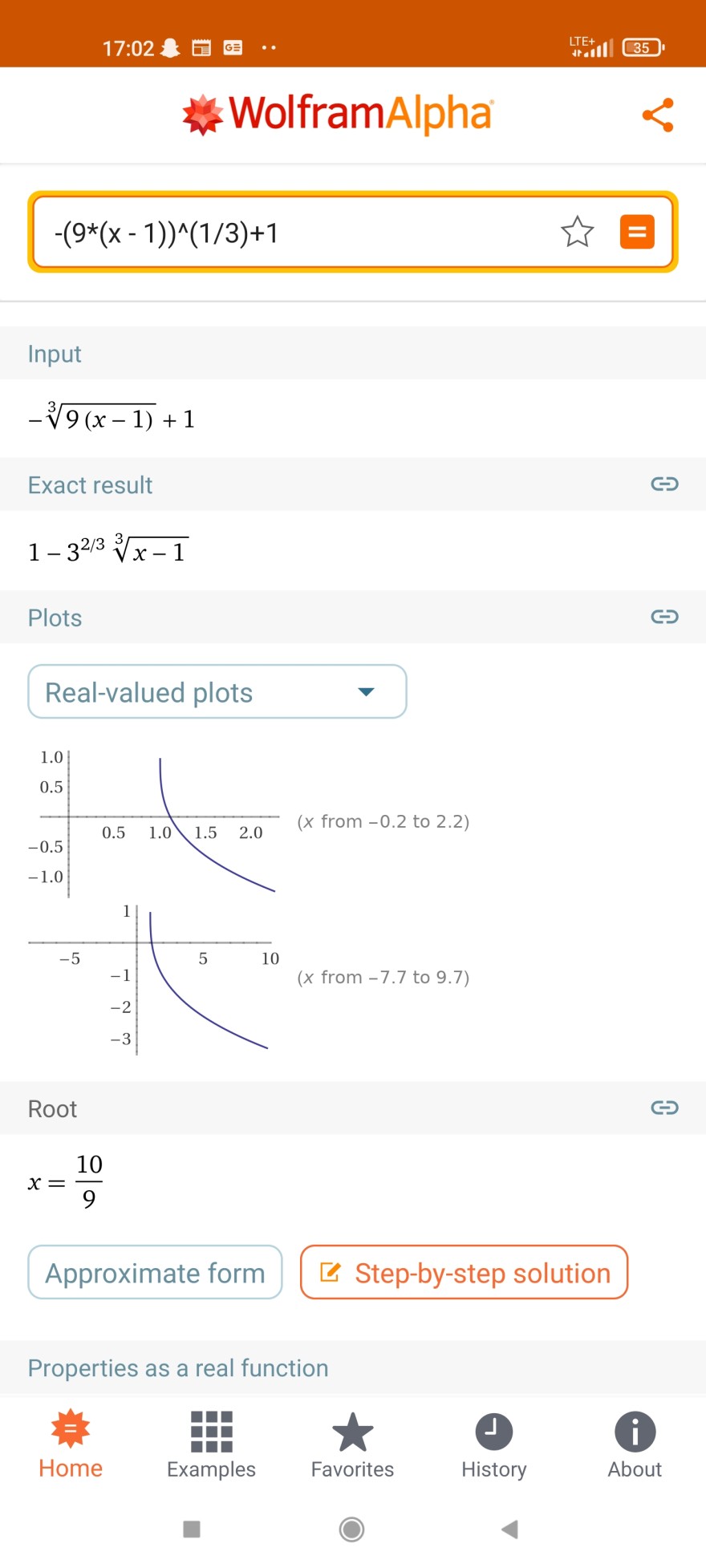

Text erkannt:

WolframAlpha
\( -(9 *(x-1))^{\wedge}(1 / 3)+1 \)
Input
\( -\sqrt[3]{9(x-1)}+1 \)
Exact result
\( 1-3^{2 / 3} \sqrt[3]{x-1} \)
Plots
Real-valued plots
Root
\( x=\frac{10}{9} \)
Approximate form
Step-by-step solution
Properties as a real function
Home
Examples
Favorites
History
About

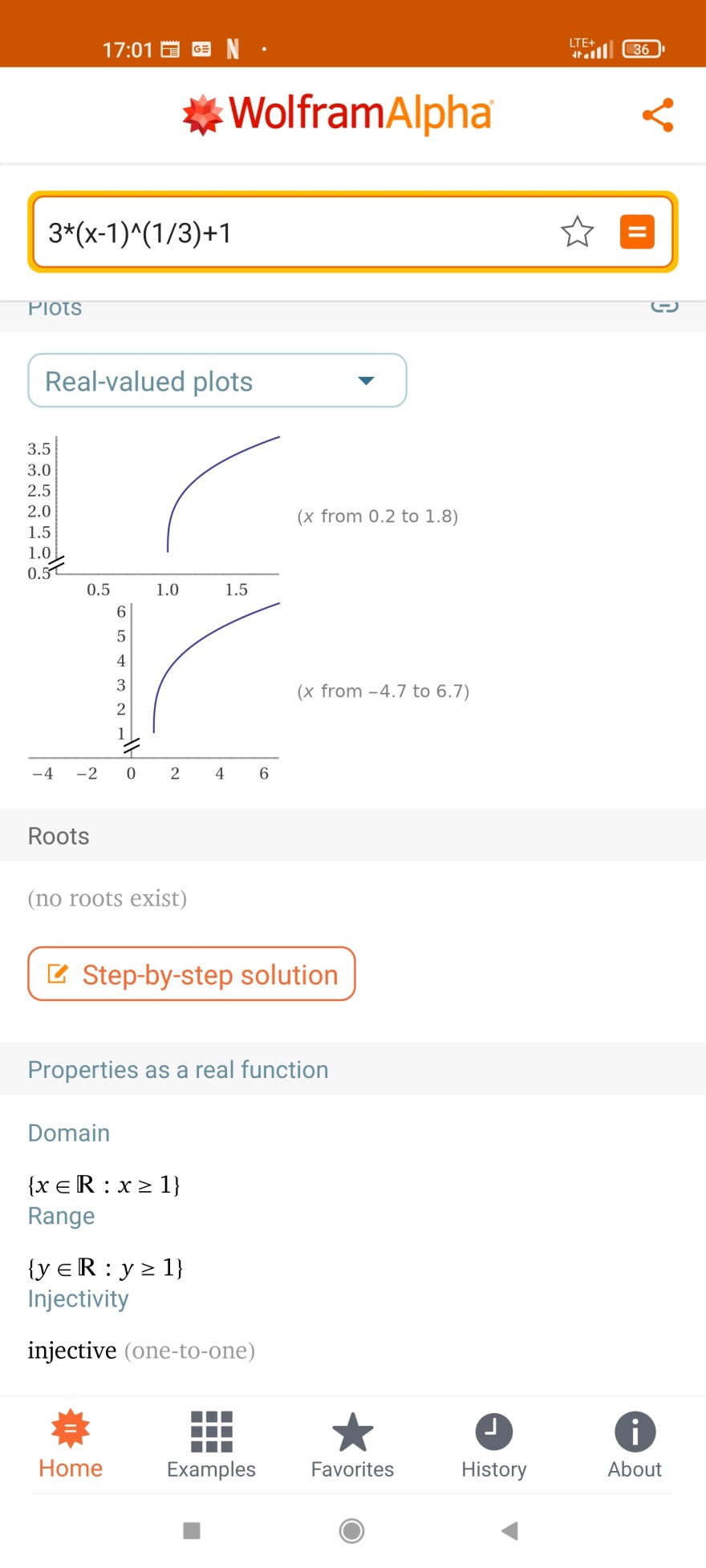
Text erkannt:

\( 3^{*}(x-1)^{\wedge}(1 / 3)+1 \)
Real-valued plots
Roots
(no roots exist)
Step-by-step solution
Properties as a real function
Domain
\( \{x \in \mathbb{R}: x \geq 1\} \)
Range
\( \{y \in \mathbb{R}: y \geq 1\} \)
Injectivity
injective (one-to-one)
Home
Examples
Favorites
History
About

Comments

Ich dachte erst an eine Potenz dritten Grades und bin zu -3(x-1)^3+1 gekommen. Da diese Potenzfunktion ja auch durch alle 3 Punkte verläuft. Aber vom Verlauf her muss es ja doch eine Wurzelfunktion sein. Also hoch (1/3)

---

Die Frage hat sich erledigt. Ich bin auf -3(x-1)^(1/3) +1 gekommen. Scheint richtig zu sein

Answer 1

Ja. Deine Funktion ist richtig.

Wie muss die Funktion ³√x geometrisch verändert werden, um die abgebildete Funktion zu erhalten

1. Spiegelung an der x-Achse

2. Streckung mit dem Faktor 3 in y-Richtung.

3. Verschiebung um eine Einheit nach rechts

4. Verschiebung um eine Einheit nach oben.

y = -3(x-1)^(1/3) +1