Ich habe die Angaben dahingehend verändert, weil der Wendepunkt bei der Parabel 3.Grades "immer in der Mitte" zwischen den Extremwerten liegt. (falls es Extremwerte gibt)
Ermitteln Sie die Funktionsgleichung 3 Grades. P1 (3,0) P1 ist ein Extremwert
Bei x= 5 liegt ein Extrempunkt, bei x= 4 ein Wendepunkt
Weg über die Nullstellenform der Parabel 3.Grades:
f(x)=a*(x-3)^2*(x-N)
f´(x)=a*[2*(x-3)*(x-N)+(x-3)^2*1]
f´(5)=a*[2*(5-3)*(5-N)+(5-3)^2]=a*[4*(5-N)+4]=a*[24-4N]
1.)a*[24-4N]=0
f´(x)=a*[(2x-6)*(x-N)+(x-3)^2]
f´´(x)=a*[2*(x-N)+(2x-6)*1+2*(x-3)]
f´´(4)=a*[2*(4-N)+(2*4-6)+2*(4-3)]=a*[2*(4-N)+2+2]=a*[12-2N]
2.) a*[12-2N]=0
N=6
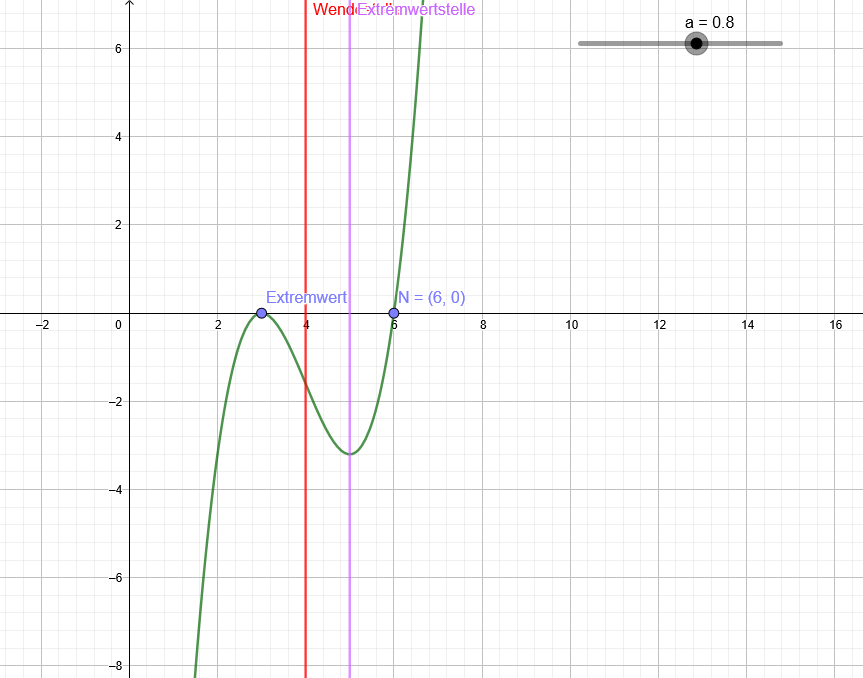
f(x)=a*(x-3)^2*(x-6) Das ist eine Parabelschar.
In der Zeichnung mit a=0,8: