Wie wird die zweite Ableitung so zusammengefasst?

Question

Aufgabe:

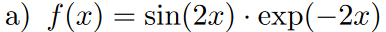
Text erkannt:

a) \( f(x)=\sin (2 x) \cdot \exp (-2 x) \)

Problem/Ansatz:

Wie wird die zweite Ableitung:

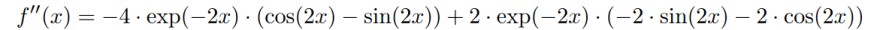
Text erkannt:

\( f^{\prime \prime}(x)=-4 \cdot \exp (-2 x) \cdot(\cos (2 x)-\sin (2 x))+2 \cdot \exp (-2 x) \cdot(-2 \cdot \sin (2 x)-2 \cdot \cos (2 x)) \)

dazu zusammengefasst:

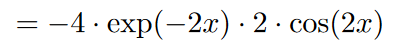
Text erkannt:

\( =-4 \cdot \exp (-2 x) \cdot 2 \cdot \cos (2 x) \)

Danke!

Text erkannt:

a) \( f(x)=\sin (2 x) \cdot \exp (-2 x) \)

Text erkannt:

a) \( f(x)=\sin (2 x) \cdot \exp (-2

Answer 1

Benutze zur Hilfe und Selbstkontrolle

https://www.ableitungsrechner.net/

Erste Ableitung

Zweite Ableitung

Answer 2

Aloha :)

Du klammerst bei der zweiten Klammer \((-2)\) aus:$$f''(x)=-4e^{-2x}(\cos2x-\sin2x)+2e^{-2x}(-2\sin2x-2\cos2x)$$$$f''(x)=-4e^{-2x}(\cos2x-\sin2x)-4e^{-2x}(\sin2x+\cos2x)$$Dann klammerst du \((-4e^{-2x})\) aus:$$f''(x)=-4e^{-2x}\left((\cos2x-\sin2x)+(\sin2x+\cos2x)\right)$$$$f''(x)=-4e^{-2x}\left(\cos2x-\sin2x+\sin2x+\cos2x\right)$$und fasst die verbliebene Klammer zusammen:$$f''(x)=-4e^{-2x}\cdot2\cos2x$$$$f''(x)=-8e^{-2x}\cdot\cos2x$$