Hallo
für kleine x kann man \( \sqrt{1-x} \) durch das 1. Taylorpolynom 1-x/2 ersetzen. (oder einfach die Funktion durch ihre Tangente in x=0 ersetzen
hier wird zu erst R^2 aus der Wurzel gezogen, dann hast du \( R*\sqrt{1-2σ/Rsinθcos(φ-μ)-σ^2/R^2 } \) dann wegen σ/R<1 kann man σ^2/R^2 ganz vernachlässigen und 2σ/Rsinθcos(φ-μ) ist das kleine x in der Formel oben .
Physiker benutzen solche linearen Näherungen gerne, weil man die linearen Funktionen besser kennt und übersehen kann.
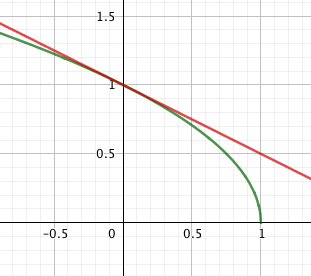
Vergleiche mein Bild, grün \(f(x)= \sqrt{1-x} \) rot die Tangente in x=0 t(x)=1-x/2
bis x=0,2 sieht man kaum einen Unterschied,
Gruß lul