Bestimmen Sie die Ableitungen f' und g'

Question

Aufgabe 10

10. Kurvenuntersuchung
Gegeben sind die Funktionen f(x) = e^0,5x und g (x) = e^(1,5x-0,25x)
a) Skizzieren Sie die Graphen von f und g in einem Koordinatensystem für -2 < x > 4
b) Bestimmen Sie die Ableitungen f' und g'
c) Wo schneiden sich die Graphen von f und g? Wie groß ist ihr Schnittwinkel?
d) Eine Ursprungsgerade h berührt den Graphen von f als Tangente. Wo liegt der Berührpunkt
von f und h? Wie lautet die Gleichung von h?
e) Wie groß ist die Fläche A, welche von f und g und der y-Achse umschlossen wird?

Kann mir jemand bitte bei dieser Aufgabe helfen ich habe sie jetzt schon 2 mal versucht und ich komme nicht auf die Lösungen die meine Lehrerin hat

Comments

Gegeben sind die Funktionen f(x) = e9,5x und g (x) = elS-025x

Das verstehe ich nicht!

---

\(f(x)=e^{9,5x}\) kann man ja noch erraten, aber bei \(g(x)\) versagt meine Glaskugel.

---

Tut mir leid ich hab es jetzt korrigiert

---

g (x) = e^(1,5x-0,25x) Stimmt das wirklich so?

---

Es gilt:

f(x) = e^(h(x)) -> f '(x) = f(x)* h'(x), Kettenregel

---

g(x)= e^1,5x-0,25x

---

Die -0,25x sind auch oben

---

Dann sieht die Funktion tatsächlich so aus?

\(g(x)=e^{1,5x-0,25x}\)

Denn das hätte man auch gleich schreiben können als

\(g(x)=e^{1,25x}\)

---

Ok wusste ich nicht

---

Oder ist g, wie von Moliets vermutet, \(g(x)=e^{1,25x^2-0,25x}\)  ?

Answer 1

f(x)=\( e^{9,5x} \)       f´(x)=\( e^{9,5x} \) *9,5

Wenn es so ist:

g (x) = e^(1,5x^2-0,25x)     g´(x)=e^(1,5x^2-0,25x)*(3x-0,25)

c) Wo schneiden sich die Graphen von f und g? Wie groß ist ihr Schnittwinkel?

\( e^{9,5x} \)=e^(1,5x^2-0,25x)

Exponentenvergleich:

9,5x=1,5x^2-0,25x

x₁=...    f(x₁)=...

x₂=...     f(x₂)=...

Comments

f(x) = \( e^{0,5x} \)             g(x)=\( e^{1,25x} \)

f´(x)= \( e^{0,5x} \)*0,5       g´(x)=\( e^{1,25x} \)*1,25

Schnittpunkte: Vergleich der Exponenten:

0,5x=1,25x

x=0    y= \( e^{0,5*0} \)  = \( e^{0} \)=1

Steigungen der beiden Tangenten :

f´(0)= \( e^{0,5*0} \)*0,5=0,5

g´(0)=\( e^{1,25*0} \)*1,25=1,25

m=|\( \frac{m₂-m₁}{1+m₁*m₂} \)|

m=|\( \frac{0,75}{1+1,25*0,5} \)|=\( \frac{6}{13} \)

\( tan^{-1} \)(\( \frac{6}{13} \))=24,78°

---

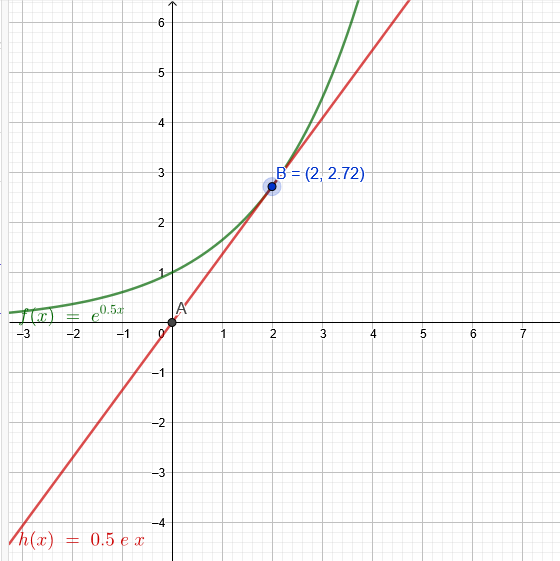
d) Eine Ursprungsgerade h berührt den Graphen von f als Tangente. Wo liegt der Berührpunkt von f und h? Wie lautet die Gleichung von h?

f(x)=\( e^{0,5x} \)     f´(x)=\( e^{0,5x} \)*0,5

\( \frac{y-0}{x-0} \)=\( e^{0,5x} \)*0,5

y=\( e^{0,5x} \)*0,5*x  geschnitten mit  f(x)=\( e^{0,5x} \)

\( e^{0,5x} \)*0,5*x=\( e^{0,5x} \)

\( e^{0,5x} \)*0,5*x-\( e^{0,5x} \)=0

\( e^{0,5x} \)*(0,5x-1)=0       \( e^{0,5x} \)≠0

(0,5x-1)=0        x=2        y=\( e^{0,5*2} \)=e

B(2|e)

f´(2)=\( e^{0,5*2} \)*0,5=0,5e

\( \frac{y-e}{x-2} \)=0,5e

h(x)=0,5e*x