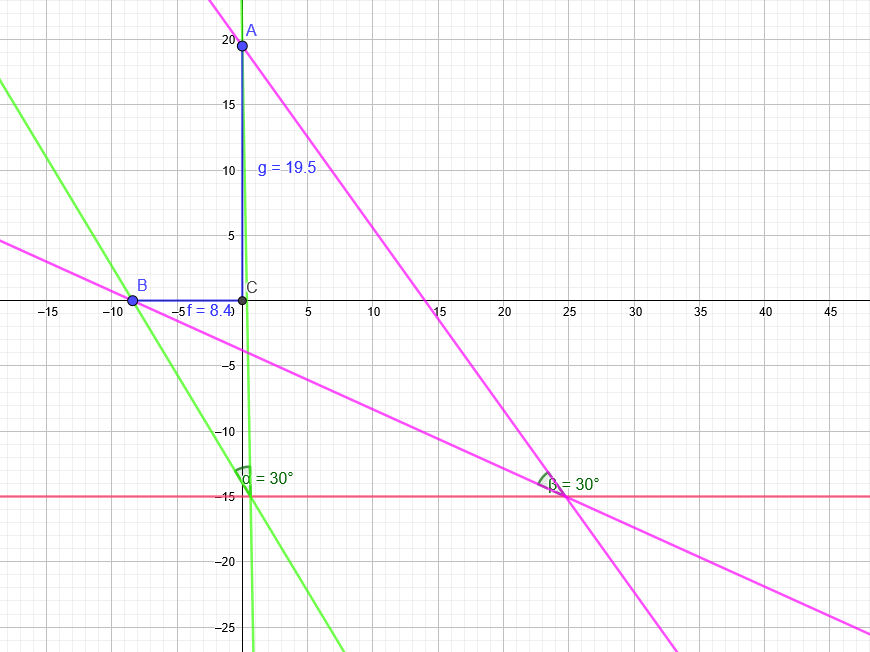
Ein Gebäude ist \( 19,50 \mathrm{~m} \) lang und \( 8,40 \mathrm{~m} \) breit. Von welchem Punkt sieht man beide Gebäudeseiten unter einem Winkel von \( 30^{\circ} \) ? Beschreibe dein Vorgehen.
Meine Festlegung:
Punkt D liegt auf der Geraden y=-15 → D(u|-15)
Steigung der Geraden durch A(0|19,5) und D(u|-15):
m₁=\( \frac{-15-19,5}{u-0} \)=\( \frac{-34,5}{u} \)
Steigung der Geraden durch B(-8,4|0) und D(u|-15):
m₂=\( \frac{-15-0}{u+8,4} \)=\( \frac{-15}{u+8,4} \)
tan(α)=|\( \frac{m₂-m₁}{1+m₁*m₂} \)|
\( \tan \left(30^{\circ}\right)=\left|\frac{-\frac{15}{u+8,4}+\frac{34,5}{u}}{1+\left(-\frac{34,5}{u}\right) \cdot\left(-\frac{15}{u+8,4}\right)}\right| \)
\( \frac{1}{3} \cdot \sqrt{3}=\left|\frac{-\frac{15}{u+8,4}+\frac{34,5}{u}}{1+\left(-\frac{34,5}{u}\right) \cdot\left(-\frac{15}{u+8,4}\right)}\right| \)
\( \frac{1}{3} \cdot \sqrt{3}=\left|\frac{-\frac{15}{u+8,4}+\frac{34,5}{u}}{1+\frac{34,5}{u^{2}+8,4 u}}\right| \)
\( \frac{1}{3} \cdot \sqrt{3}=\left|\frac{\frac{34,5 \cdot(u+8,4)-15 u}{u^{2}+8,4 u}}{\frac{u^{2}+8,4 u+34,5 \cdot 15}{u^{2}+8,4 u}}\right| \)
\( \frac{1}{3} \cdot \sqrt{3}=\left|\frac{34,5 \cdot(u+8,4)-15 u}{u^{2}+8,4 u+34,5 \cdot 15}\right|=\left|\frac{19,5 u+289,8}{u^{2}+8,4 u+517,5}\right| \)
\( u_{1} \approx 0,63 \)
\( u_{2} \approx 24,75 \)