Hallo Leute, kann mir jemand helfen?
1a) In der empirischen Sozialforschung dient die Durchführung eines Signifikanztest nicht dazu, um herauszufinden wie stark ein Zusammenhang zwischen zwei oder mehreren gemessenen Merkmalen ist, bzw. wie groß ein gemessener Unterschied zwischen zwei oder mehreren Gruppen bezüglich eines Merkmals ist. (Richtig oder Falsch)
b) Mit einem Signifikanztest kann man anhand des errechneten Ergebnisses in der Stichprobe feststellen, mit welcher Wahrscheinlichkeit die Nullhypothese zutrifft. (Richtig/Falsch/Kommt drauf an wie sehr signifikant das Ergebnis ist/Gilt nur für Unterschiedshypothesen).
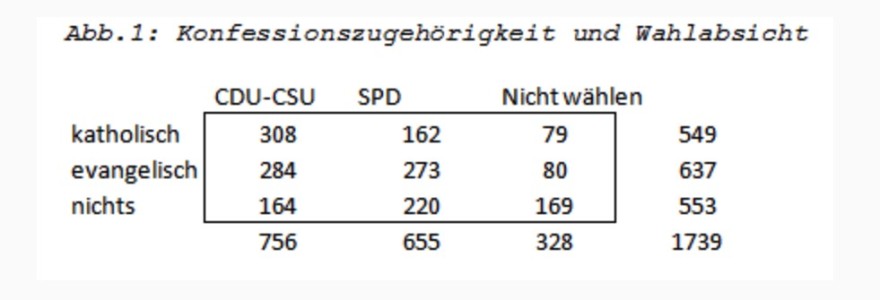
Eine Forschergruppe prüft das politische Verhalten von Menschen unterschiedlicher Konfessionen. Dabei schauen Sie sich das Wahlverhalten der jeweiligen Gruppen an. Hierzu wird eine repräsentative, deutschlandweit durchgeführte Umfrage genutzt. Die Häufigkeiten für eine bekundete Wahl für die CDU-CSU und für die SPD ist für Katholiken, Evangelen und Konfessionslose abgetragen.
Text erkannt:
Abb.1: Konfessionszugehörigkeit und Wahlabsicht katholis evangelisc nichts
Bestimmen Sie mit einem geeigneten Test, ob beide Merkmale statistisch unabhängig voneinander sind.
a)
Welchen Wert für die Teststatistik haben Sie berechnet? Geben Sie diesen mit zwei Stellen nach dem Dezimalpunkt an.
b)
Für wie viele Freiheitsgrade wird die Teststatistik auf Signifikanz überprüft? (Angabe ohne Dezimalstellen)
c)
Mit welcher Realisierungswahrscheinlichkeit ist dieser oder ein noch größerer Effekt bei Geltung der Nullhypothese zu erwarten? (ca. 1,0%, ca. 0,0%, ca. 0.2%, ca. 1,2%)
d)
Beurteilen Sie die folgende Aussage: "Das heißt, dass der bivariate Zusammenhang zwischen diesen beiden Merkmalen in der Population nur mit einer Wahrscheinlichkeit von ca. x%(x ist hier Ihr Wert aus der vorigen Aufgabe) anders ist, als der in ihrer Stichprobe." (Richtig oder Falsch)
Komme leider nicht weiter:
Für Chi ^2 habe ich folgendes Ergebnis (20.1405+9.6985+5.8201+0.1808+4.5587+13.4152+24.2840+0.6584+40.1292)
=118.8854
Freiheitsgrade =(z−1)x(x−1)=(3−1)x(3−1)=4
kritischer Chi-Wert bei df=4: 9.488. aus der Tabelle
Komme bei den beiden Fragen nicht weiter: Welchen Wert für die Teststatistik haben Sie berechnet? Für wie viele Freiheitsgrade wird die Teststatistik auf Signifikanz überprüft?
Wie wird dies berechnet?
FG