Oberstufenschüler verwenden ein elektronisches Werkzeug, wenn sie Mathematikaufgaben lösen. Dieses Werkzeug wird meistens nur als Rechenknecht verwendet. Im folgenden Beispiel soll die Verwendung eines GTR dem mathematischen Wissensgewinn dienen:
1. Die Schüler*innen erhalten eine Übersicht über Graphen einiger prototypischer Funktionen:
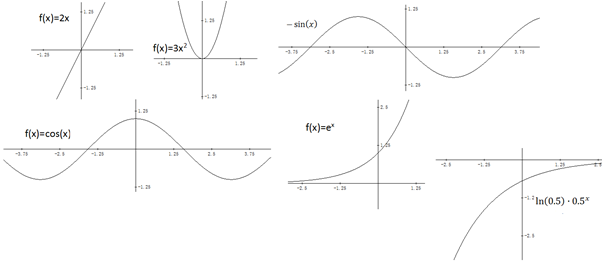
1. Aufgabe: Welchen Funktionsgraphen erwartest du für f(x)=\( \frac{(x+0.01)^{2}-x^2}{0.01} \) ? Zeichne den Graphen mit dem GTR und vergleiche mit den Graphen zu 1. Was schließt du aus dem Ergebnis und warum?
2. Aufgabe: Welchen Funktionsgraphen erwartest du für f(x)=\( \frac{(x+0.01)^3-x^3}{0.01} \) ? Zeichne den Graphen mit dem GTR und vergleiche mit den Graphen zu 1. Was schließt du aus dem Ergebnis und warum?
3. Zeichne den Graphen von f(x)=\( \frac{sin(x+0.01)-sin(x)}{0.01} \) mit dem GTR und vergleiche ihn mit den Graphen zu 1. Was schließt du daraus? Begründe.
4. Zeichne den Graphen von f(x)=\( \frac{cos(x+0.01)-cos(x)}{0.01} \) mit dem GTR und vergleiche ihn mit den Graphen zu 1. Was schließt du daraus? Begründe.
5. Zeichne den Graphen von f(x)=\( \frac{e^{x+0.01}-e^x}{0.01} \) mit dem GTR und vergleiche ihn mit den Graphen zu 1. Was schließt du daraus? Begründe.
6. Zeichne den Graphen von f(x)=\( \frac{0.5^{x+0.0}-5.5^x}{0.05} \) mit dem GTR und vergleiche ihn mit den Graphen zu 1. Was schließt du daraus? Begründe.