Hallo Paula,
mit \(y \in \mathbb V\) ist sicher ein Punkt in einem Vektorraum gemeint. Mit Ursprungsgerade durch \(x\) - noch ein Punkt, also \(x \in\mathbb V\) - ist eine Gerade gemeint, die durch den Ursprung (Koordinatennullpunkt) und durch den Punkt \(x\) geht. Die Anzahl der Dimensionen von \(\mathbb V\) soll hier keine Rolle spielen. Aber man kann es sich im 2-dimensionalen mal skizzieren:
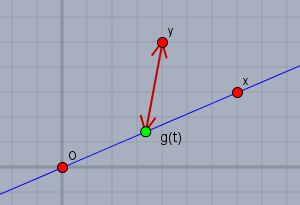
Die Gerade ist mit \(g(t)\) beschreiben und ein bestimmtes \(t\) beschreibt einen Punkt auf der Geraden - z.B. den grünen Punkt. Der Abstand \(a\) von irgendeinem Punkt mit Parameter \(t\) zum Punkt \(y\) ist$$a(t) = \|y-g(t)\|$$Und die Funktion \(f(t)\) soll das Quadrat des Abstands beschreiben, also:$$f(t) = \|y-g(t)\|^2$$und für diese Funktion soll das Minimum gefunden werden. Zur Schreibweise: das Skalarprodukt zweier Vektoren \(a\) und \(b\) ist \(\left<a,\,b\right>\) und dies ist identisch mit \(a^T\cdot b\) in Vektorschreibweise. So ergibt sich für die Funktion \(f\) und ihre Ableitung:$$\begin{aligned} f(t) &= \|y-g(t)\|^2 \\&= \left<y-g(t),\,y-g(t)\right> \\ &= \left<y,\,y\right> -2\left<y,\,g(t)\right> + \left<g(t),\,g(t)\right> \\ f'(t) &= -2\left<y,\,g'(t)\right>+2\left<g(t),\,g'(t)\right> \\&= 2\left<g(t) - y,\, g'(t)\right>\\ \end{aligned}$$an der letzten Gleichung kann man schon sehen, dass ein Optimum genau dann erreicht wird, wenn das angegeben Skalarprodukt =0 ist, d.h. dass der Verbindungsvektor \((g(t)-y)\) senkrecht auf der Richtung der Geraden stehen muss.
Da \(g(t)\) eine Urspungsgerade durch den Punkt \(x\) sein soll, kann man schreiben$$g(t) = xt \quad g'(t) =x$$Einsetzen in \(f'(t)\) und Nullsetzen der Ableitung gibt$$\begin{aligned}f(t_{\operatorname{opt}}) &=-2\left<y,\,g'(t_{\operatorname{opt}})\right>+2\left<g(t_{\operatorname{opt}}),\,g'(t_{\operatorname{opt}})\right> \\&= -2\left<y,\,x\right> + 2\left<xt_{\operatorname{opt}},\,x\right> \to 0\\\implies t_{\operatorname{opt}}&= \frac{\left<y,\,x\right>}{\left<x,\,x\right>}\end{aligned}$$Da dieser Term eindeutig und für \(x \ne \vec 0\) immer definiert ist, gibt es genau eine Lösung für \(t\) und damit genau einen Punkt auf \(g\), der \(y\) am nächsten liegt.
zu b) Die Abbildung \(P\) ist die Abbildung von \(y\) auf \(g(t_{\operatorname{opt}})\). Dazu setze zunächst den Wert für \(t_{\operatorname{opt}}\) in \(g(t)\) ein, was den zu \(y\) nächstgelegenden Punkt auf \(g\) ergibt:$$\begin{aligned}g(t_{\operatorname{opt}})&=\frac{\left<y,\,x\right>}{\left<x,\,x\right>}x \\&= \frac1{\left<x,\,x\right>} \cdot x\left<x,\,y\right> \\&= \frac1{\left<x,\,x\right>} \cdot x\cdot x^T\cdot y\\&= \frac1{\left<x,\,x\right>} \cdot\left( x \otimes x\right)\cdot y\\\end{aligned}$$Der Ausdruck \(\left( x \otimes x\right)\) ist das dyadische Produkt und ein Matrix. Also ist \(P\)$$P:\quad y \to g(t_{\operatorname{opt}}) = \underbrace{\frac1{\left<x,\,x\right>} \cdot\left( x \otimes x\right)}_{=M}\cdot y = My$$Damit ist die Abbildung \(P\) eine Matrix-Vektor-Muiltiplikation und daher linear. Dass \(P = P \circ P\) ist, lässt sich mittels Vektorschreibweise zeigen$$\begin{aligned}P\circ P \to M \cdot M &= \frac1{\left<x,\,x\right>} xx^T \cdot \frac1{\left<x,\,x\right>} xx^T \\&= \frac{x \cdot x^T \cdot x \cdot x^T}{\left<x,\,x\right> \cdot \left<x,\,x\right>} \\&= \frac{x\cdot \left< x,\,x\right> \cdot x^T}{\left<x,\,x\right> \cdot \left<x,\,x\right>}\\&= \frac{x\cdot x^T}{\left<x,\,x\right>} \\&= M\end{aligned}$$
... und dass für alle y,z ∈ V die Eigenschaft ⟨P(y),z⟩ = ⟨y,P(z)⟩ gilt (d.h. P ist selbstadjungiert).
.. mache ich vielleicht morgen; jetzt ist es zu spät
Gruß Werner