Zunächst eine Skizze:
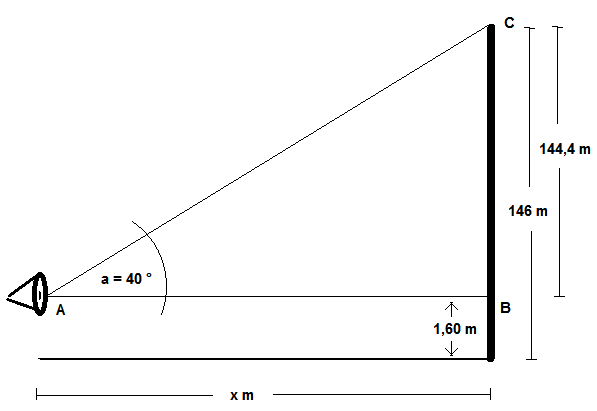
(Der fette senkrechte Strich auf der rechten Seite stellt den Funkturm dar. Der "Trichter" auf der linken Seite soll das Auge darstellen, welches sich in 1,60 m Höhe und x Meter vom Funkturm entfernt befindet. befindet.)
Das Dreieck ABC ist rechtwinklig, deswegen kann man einfache trigonometrische Sätze anwenden. In diesem Fall bietet sich die Beziehung
tan ( a ) = Gegenkathete / Ankathete
an. Gegenkathete ist die Strecke BC, Ankathete ist die Strecke AB, deren Länge gesucht wird. Die Formel sieht also bezogen auf das vorliegende Beispiel so aus:
tan ( a ) = BC / AB
Auflösen der Formel nach AB:
<=> AB = BC / tan ( a )
Bekannte Werte einsetzen:
AB = 144,4 / tan ( 40 ° ) = 172,089...
Die Entfernung des Auges des Betrachters vom Funkturm muss also etwa 172 Meter betragen, damit er ihn unter einem Höhenwinkel von 40 ° sieht.