Sieht wohl so aus:
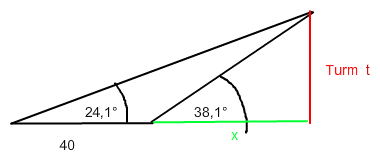
tan(24,1°) = t / (40+x) und tan(38,1°) = t / x
===> t = x* tan(38,1°) =0,7841x #
0,4473 = 0,7841x / (40+x)
<=> 0,4473* (40+x) = 0,7841x
<=> 17,89 + 0,4473x = 0,7841x
<=> 17,89 = 0,3368x
<=> x = 53,12
==> (mit # ) t = 41,65
plus die Augenhöhe
==> Turm ist 43,25 m hoch.