Aufgabe:
Bestimmen Sie für die folgenden Funktionen die Menge aller Punkte, in denen
sie stetig sind.
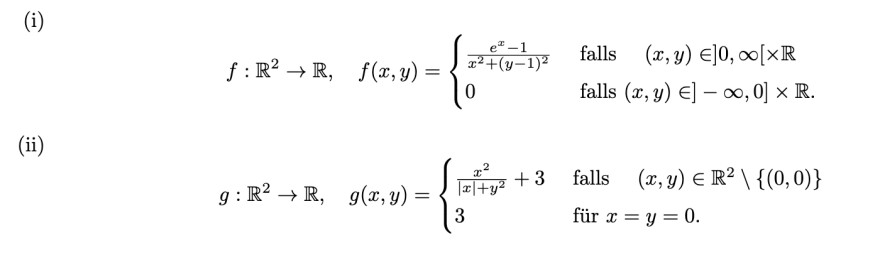
Text erkannt:
(i)
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad f(x, y)=\left\{\begin{array}{ll} \frac{e^{x}-1}{x^{2}+(y-1)^{2}} & \text { falls } \quad(x, y) \in] 0, \infty[\times \mathbb{R} \\ 0 & \text { falls }(x, y) \in]-\infty, 0] \times \mathbb{R} \end{array}\right. \)
(ii)
\( g: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad g(x, y)=\left\{\begin{array}{ll} \frac{x^{2}}{|x|+y^{2}}+3 & \text { falls } \quad(x, y) \in \mathbb{R}^{2} \backslash\{(0,0)\} \\ 3 & \text { für } x=y=0 . \end{array}\right. \)
Problem/Ansatz:
als erstes würde ich die stetigkeit beider kompositionen bestimmen, aber hab keinen plan wie..
vielen dank im voraus
Text erkannt:
(i)
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad f(x, y)=\left\{\begin{array}{ll} \frac{e^{x}-1}{x^{2}+(y-1)^{2}} & \text { falls } \quad(x, y) \in] 0, \infty[\times \mathbb{R} \\ 0 & \text { falls }(x, y) \in]-\infty, 0] \times \mathbb{R} \end{array}\right. \)
(ii)
\( g: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad g(x, y)=\left\{\begin{array}{ll} \frac{x^{2}}{|x|+y^{2}}+3 & \text { falls } \quad(x, y) \in \mathbb{R}^{2} \backslash\{(0,0)\} \\ 3 & \text { für } x=y=0 . \end{array}\right. \)