Aufgabe:
Text erkannt:
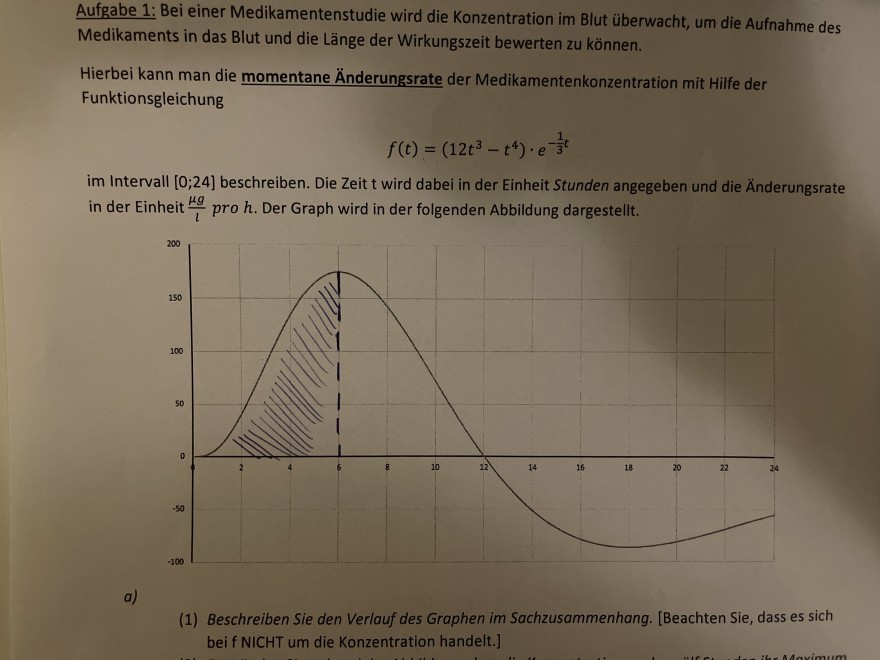
Aufgabe 1: Bei einer Medikamentenstudie wird die Konzentration im Blut überwacht, um die Aufnahme des Medikaments in das Blut und die Länge der Wirkungszeit bewerten zu können.
Hierbei kann man die momentane Änderungsrate der Medikamentenkonzentration mit Hilfe der Funktionsgleichung
\( f(t)=\left(12 t^{3}-t^{4}\right) \cdot e^{-\frac{1}{3} t} \)
im Intervall \( [0 ; 24] \) beschreiben. Die Zeit t wird dabei in der Einheit Stunden angegeben und die Änderungsrate in der Einheit \( \frac{\mu g}{l} \) pro \( h \). Der Graph wird in der folgenden Abbildung dargestellt.
a)
(1) Beschreiben Sie den Verlauf des Graphen im Sachzusammenhang. [Beachten Sie, dass es sich bei f NICHT um die Konzentration handelt.]

Text erkannt:
h) Berechnen Sie den maximalen Wert def Konzentration. [Beachten Sie a) (2)!]
i) Berechnen Sie den Wert der Konzentration nach 24 Stunden.
Beurteilen Sie, ob man mit der Funktion \( F(t)=3 t^{4} \cdot e^{-\frac{1}{3} t} \) den Verlauf der Konzentration beschreiben kann. [Haben Sie \( F(0) \) beachtet?]
Problem:
Ich verstehe nicht genau, was ich bei h),i), und j) genau machen muss.
Ein nachvollziehbarer Lösungsweg würde mir sehr helfen.
Lg