Ableitung einer gebrochenrationalen Funktion mit Buchstaben + Null setzen

Question

,

 

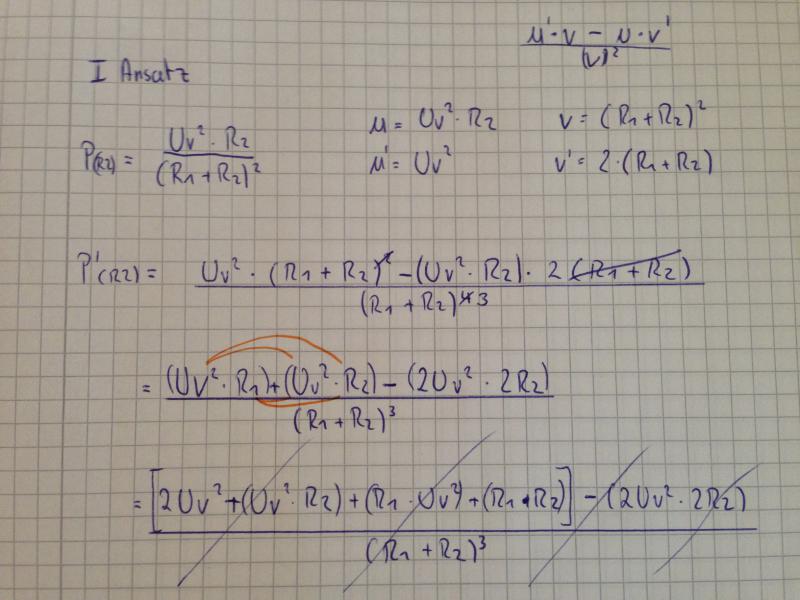
ich habe ein Problem bei folgender Funktion (Bild).

 

Diese soll abgeleitet werden und dann Null gesetzt werden. Habe mich mal dran probiert und möchte mich jetzt erkundigen, ob dieser Ansatz richtig ist und ob mir einer die Funktion nachvollziehbar ableiten und Null setzen kann.

Vielen lieben Dank im Voraus!

Answer 1

Das ist soweit richtig. Ich würde hinten noch 2 wieder ausklammern. Dann entsteht:

$$ \frac { ({U}_{V}^2 * {R}_{1}) +  ({U}_{V}^2 * {R}_{2}) - 2 ({U}_{V}^2 * {R}_{2}) } { ({R}_{1}+ {R}_{2})^3 } $$
= $$ \frac { ({U}_{V}^2 * {R}_{1}) -  ({U}_{V}^2 * {R}_{2}) } { ({R}_{1}+ {R}_{2})^3 } $$

Jetzt noch $$ {U}_{V}^2 $$ ausklammern:

$$ \frac { {U}_{V}^2 * ({R}_{1} - {R}_{2}) } { ({R}_{1}+ {R}_{2})^3 } $$

 

Jetzt siehst du, dass R₂ = R₁ sein muss, damit die Ableitung 0 ist.

Answer 2

bis zu dieser Zeile stimmt es noch

P ´( R2 ) = [ Uv^2 * ( R1 + R2 ) - 2 * Uv^2 * R2 ] / ( R1 + R2 )^3
P ´( R2 ) = Uv^2 * [ R1 + R2  - 2 * R2 ] / ( R1 + R2 )^3
P ´( R2 ) = Uv^2 * [ R1 - R2 ] / ( R1 + R2 )^3
Extremwert
Uv^2  * [ R1 - R2 ] / ( R1 + R2 )^3  = 0
das heißt der Zähler ist null
R1 -R2 = 0
R2 = R1

P ( R1 ) = ( Uv^2 * R1 ) / ( R1 + R1)^2
P ( R1 ) = ( Uv^2 * R1 ) / ( 4 * R1^2 ) = Uv^2 / ( 4 * R1 )

E ( R1 l  Uv^2 / ( 4 * R1 ) )

Bei Fehlern oder Fragen wieder melden.

mfg Georg