Aufgabe:
Ich muss ein Lemma von Miller-Rabin Primzahltest beweisen. Mir wurde gesagt dass der Beweis an einigen Stellen nicht ganz richtig ist. Ich brauche nun eine Korrektur des Beweises.
Problem/Ansatz:
Text erkannt:
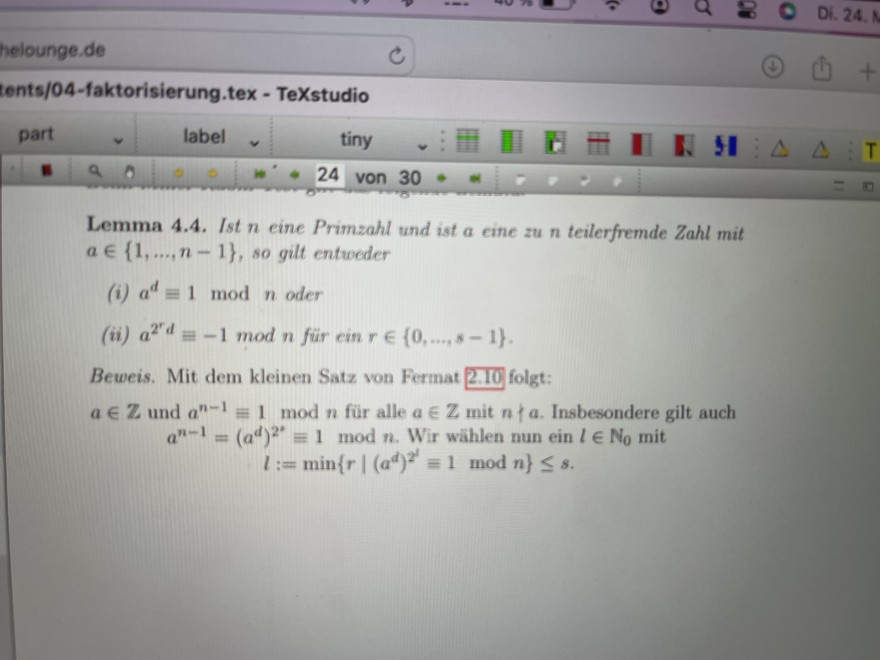
Lemma 4.4. Ist \( n \) eine Primzahl und ist a cine su \( n \) teilerfremde Zahl mit \( a \in\{1, \ldots, n-1\}, s o \) gilt entwoder
(i) \( a^{d} \equiv 1 \bmod n \) oder
(ii) \( a^{2^{r} d} \equiv-1 \bmod n \) für ein \( r \in\{0, \ldots, s-1\} \).
Beweis. Mit dem kleinen Satz von Fermat \( 2.10 \) folgt:
\( a \in \mathbb{Z} \) und \( a^{n-1} \equiv 1 \bmod n \) für alle \( a \in \mathbb{Z} \) mit \( n \nmid a \). Insbesondere gilt auch \( a^{n-1}=\left(a^{d}\right)^{2^{s}} \equiv 1 \) mod \( n \). Wir wählen nun ein \( l \in N_{0} \) mit
\( l:=\min \left\{r \mid\left(a^{d}\right)^{2^{l}} \equiv 1 \bmod n\right\} \leq s \text {. } \)

Text erkannt:
KAPITEL 4. PRIMZAHLTESTS
19
Dann gilt:
1. Fall: \( l=0 \Leftrightarrow a^{d} \equiv 1 \bmod n \). Damit gilt (i).
2. Fall: Für \( l \neq 0 \), also \( 0<l \leq s \) gilt: \( \left(a^{d}\right)^{2^{d-1}} \neq 1 \bmod n \). Der Einfachheit halber definieren wir \( b:=\left(a^{d}\right)^{2^{-1}} \neq 1 \bmod n \). Dann ist \( b^{2}= \) \( \left(\left(a^{d}\right)^{2^{1}}\right) \equiv 1 \bmod n \). Das bedeutet, dass \( b^{2}-1 \equiv 0 \bmod n \) ist.
Also folgt mit \( n \in \mathbb{P}(b+1)(b-1) \Rightarrow\left\{\begin{array}{l}b+1=0 \bmod n \\ b-1 \equiv 0 \bmod n\end{array}\right. \)
Da \( b-1 \equiv 0 \bmod n \) ein Wiederspruch zu \( b=\left(a^{d}\right)^{2^{l-1}} \not \equiv 1 \bmod n \) ist, folgt \( \left(a^{d}\right)^{2^{2-1}}=b \equiv-1 \bmod n \). Mit \( r:=l-1 \) folgt (ii) und damit die Behauptung.
Das Lemma besagt also, wenn