ich frage mich ob das Integral von 0,4x das Gleiche ist, wenn man 0,4 zuvor ausklammern oder eben nicht.
Folgendes Integral soll gebildet werden:
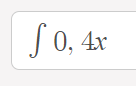
Text erkannt:
\( \int 0,4 x \)
Wenn ich es ausklammere, lautet das Ergebnis:
0,4*(x^2 / 2)
Nun möchte ich, wissen wie der Rechenweg lautet, wenn ich die Ausklammerung auslassen würde.
Sprich:
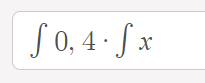
Text erkannt:
\( \int 0,4 \cdot \int x \)
Integral von 0,4 = 0,4x
und Integral von x = x^2/2
Dort erhalte ich, wenn beispielweise für 0 bis 8 (Intervall) integriert wird, aber unterschiedliche Ergebnisse.
Wo habe ich den Verständnisfehler?