Der Effektivwert \( U_{e f f} \) einer Spannung kann berechnet werden mittels \( U_{e f f}=\sqrt{\frac{1}{T} \int \limits_{0}^{T} u(t)^{2} \mathrm{~d} t \text {. }} \)
Berechnen Sie den Effektivwert der folgenden Spannungen. Mit \( U_{a m p}=7 \mathrm{~V}, U_{1}=9 \mathrm{~V}, U_{2}=-7 \mathrm{~V} \) und \( T_{1}=2 \mathrm{~s}<T \).
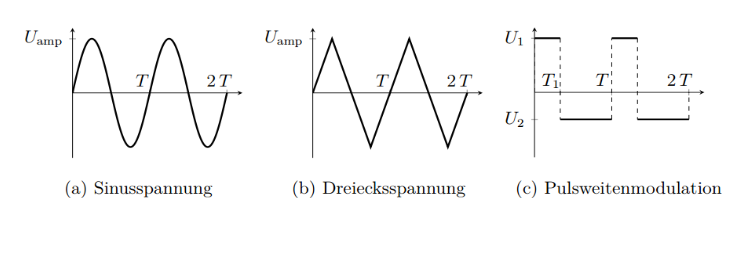
(a) Geben Sie die Funktionsgleichung für die Spannung \( u(t) \) an.
1- u(t)=
2- Ueff=
3- Ueff=
4- Ueff=