Zeigen Sie, dass die Funktion g eine Reduktion ist

Question

Aufgabe:

Es seien die folgenden Entscheidungsprobleme gegeben:

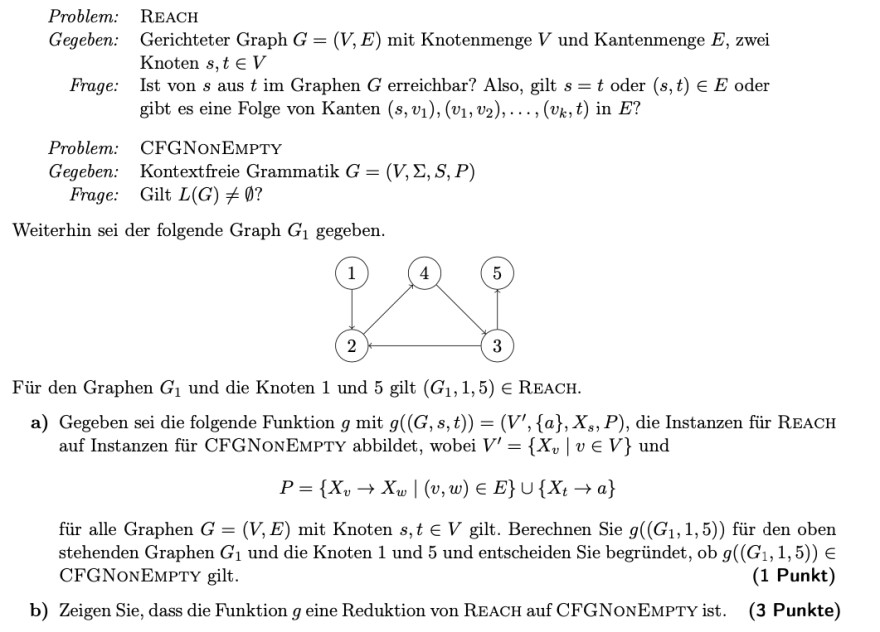
Text erkannt:

Problem: REACH
Gegeben: Gerichteter Graph \( G=(V, E) \) mit Knotenmenge \( V \) und Kantenmenge \( E \), zwei Knoten \( s, t \in V \)

Frage: Ist von \( s \) aus \( t \) im Graphen \( G \) erreichbar? Also, gilt \( s=t \) oder \( (s, t) \in E \) oder gibt es eine Folge von Kanten \( \left(s, v_{1}\right),\left(v_{1}, v_{2}\right), \ldots,\left(v_{k}, t\right) \) in \( E \) ?
Problem: CFGNONEMPTY
Gegeben: \( \quad \) Kontextfreie Grammatik \( G=(V, \Sigma, S, P) \)
Frage: Gilt \( L(G) \neq \emptyset \) ?
Weiterhin sei der folgende Graph \( G_{1} \) gegeben.
Für den Graphen \( G_{1} \) und die Knoten 1 und 5 gilt \( \left(G_{1}, 1,5\right) \in \) REACH.
a) Gegeben sei die folgende Funktion \( g \) mit \( g((G, s, t))=\left(V^{\prime},\{a\}, X_{s}, P\right) \), die Instanzen für REACH auf Instanzen für CFGNonEmPTY abbildet, wobei \( V^{\prime}=\left\{X_{v} \mid v \in V\right\} \) und
\( P=\left\{X_{v} \rightarrow X_{w} \mid(v, w) \in E\right\} \cup\left\{X_{t} \rightarrow a\right\} \)
für alle Graphen \( G=(V, E) \) mit Knoten \( s, t \in V \) gilt. Berechnen Sie \( g\left(\left(G_{1}, 1,5\right)\right) \) für den oben stehenden Graphen \( G_{1} \) und die Knoten 1 und 5 und entscheiden Sie begründet, ob \( g\left(\left(G_{1}, 1,5\right)\right) \in \) CFGNONEMPTY gilt.
(1 Punkt)
b) Zeigen Sie, dass die Funktion \( g \) eine Reduktion von REACH auf CFGNONEMPTY ist. (3 Punkte)

Ich verstehe leider gar nicht, was ich hier machen soll, wie berechne ich g((G_1 ,1,5)), wie Entscheide ich danach, ob es eine Reduktion ist? Kann mir jemand helfen? Ich bin am verzweifeln.