Kurvendiskussion von f(x) = 2sin(x-π/3)-1. Trigonometrische Funktion

Question

Hallo ihr lieben,

könnt ihr mir sagen was ich falsch gemacht habe und wo meine Fehler liegen?

Ich soll eine Kurvenuntersuchung bei der funktion durchfühlen.

 

Ich hoffe ihr könnt meine Schrift lesen.

Hoffe auf tolle Antworten von euch. :-) 

Comments

f (x) = 2sin(x-π/3) - 1

f ' (x) = 2cos(x-π/3)            
Bei der Ableitung fällt -1 weg, da (-1) eine Konstante ist.

Kontrolle mit https://www.wolframalpha.com/input/?i=+f%28x%29+%3D+2sin%28x-π%2F3%29-1

zeigt dir, ob deine Resultate stimmen können. Zwischenresultate können aber anders aussehen, da WolframAlpha sin in cos umwandelt.

Answer 1

f(x) = 2·SIN(x - pi/3) - 1

f'(x) = 2·COS(x - pi/3)

f''(x) = - 2·SIN(x - pi/3)

Eigentlich diskutierst du hier eine Sinusfunktion die um den Faktor 2 gestreckt, um pi/3 nach rechts verschoben und dann um eine Einheit nach unten verschoben worden ist.

Du kannst also die bekannten extrem und Wendepunkte der Sinusfunktion ebenso Transformieren und erhältst die markanten Punkte der Funktion f.

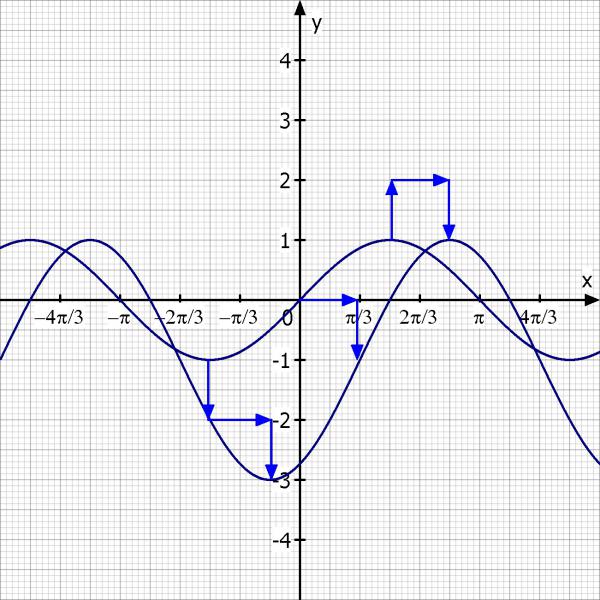
Ich zeichne mal die normale Sinusfunktion und f(x) in ein Koordinatensystem, sodass du die Transformation nachvollziehen kannst.