Fläche mit Doppelintegral lösen

Question

Aufgabe:

Die Aufgabenstellung unten im Bild.

Problem/Ansatz:

Hallo,
wer kann mir helfen diese Aufgabe zu lösen?
Wie gehe ich bei dieser Aufgabe vor?
Mit dem gegebenen Integral kann ich leider auch nicht so viel anfangen..

Ich würde mich extrem über einige lösungsansätze/tipps freuen..


Gruß

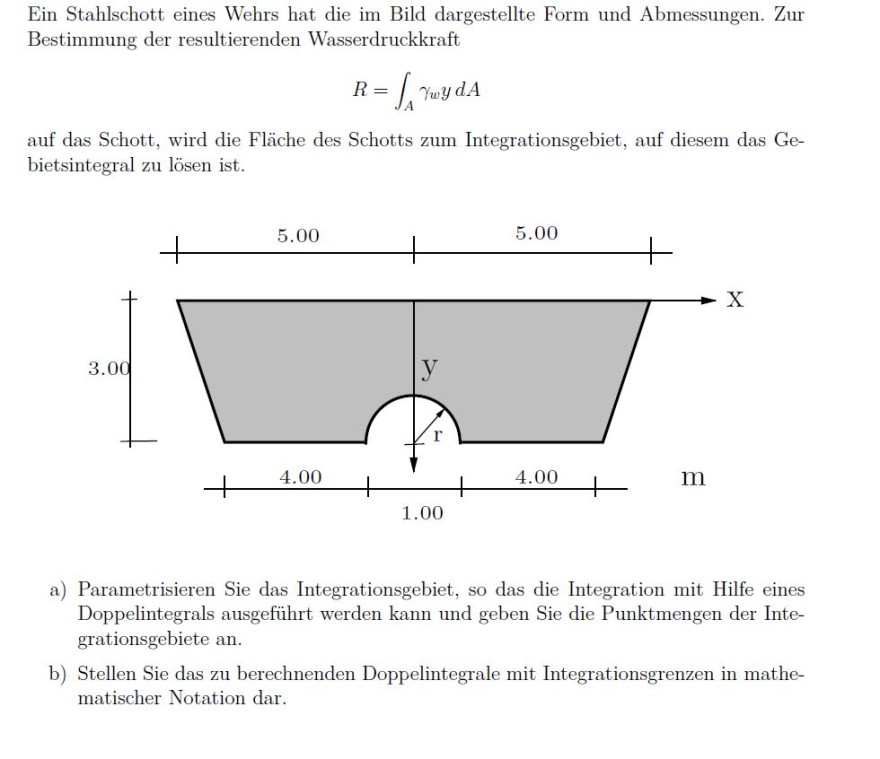
Text erkannt:

Ein Stahlschott eines Wehrs hat die im Bild dargestellte Form und Abmessungen. Zur Bestimmung der resultierenden Wasserdruckkraft
\( R=\int \limits_{A} \gamma_{w} y d A \)
auf das Schott, wird die Fläche des Schotts zum Integrationsgebiet, auf diesem das Gebietsintegral zu lösen ist.
a) Parametrisieren Sie das Integrationsgebiet, so das die Integration mit Hilfe eines Doppelintegrals ausgeführt werden kann und geben Sie die Punktmengen der Integrationsgebiete an.
b) Stellen Sie das zu berechnenden Doppelintegrale mit Integrationsgrenzen in mathematischer Notation dar.

Answer 1

Hallo

du teilst das Gebiet von y=0 bis 5 in 3 Teile, von x=0 bis 1/2 hast du die Fläche unter y=-√(1/2-x^2)+3

dann die Flache unter y=3 von1/2 bis bis 4,5 dann von 4,5 bis 5 die Fläche unter y=-6x+30

da die Figur symmetrisch zu x=0 kannst du dann das Integral verdoppeln

Gruß lul

Comments

Hallo,

danke für die Antwort.

Die Gebietseinteilung verstehe ich.

Könntest du bitte erklären wie du die funktionen hergeleitet hast ?

vielen dank

Gruß

---

Hallo

 1, der Kreis: Mittelpunkt  bei (0,3), Radius abgelesen o,5

2. Gerade: Steigung ablesen 3/-0,5. daraus y=-6x+b- Punkt (0,5) einsetzen für b.

Gruss lul