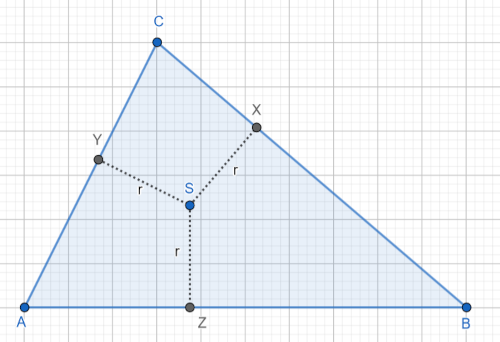
Für den Innenkreisradius r gilt aufgrund der Formel von Heron:
\( r^2 = \frac{(s-a)(s-b)(s-c)}{s} \) mit \( s = \frac{a+b+c}{2} \)
Weiter gilt:
\( AY + CY + CX + BX + BZ + AZ = a+b+c = 2s \)
Aufgrund der Symmetrie AY = AZ, BX = BZ, CX = CY folgt:
\( AZ + BX + CY = s \)
Daraus folgt:
\( AZ = s - BX - CY = s - (BX+CY) = s - (BX+CX) = s - a \)
\( BX = s - AZ - CY = s - (AZ+CY) = s - (AY+CY) = s - b \)
\( CY = s - BX - AZ = s - (BX+AZ) = s - (BZ + AZ ) = s - c \)
Da YS, XS, ZS jeweils senkrecht auf a,b,c stehen folgt:
\( AS^2 = r^2 + AZ^2 = r^2 + (s-a)^2 = \frac{1}{s}*((s-a)(s-b)(s-c)+ s(s-a)^2) \)
\( BS^2 = r^2 + BX^2 = r^2 + (s-b)^2 = \frac{1}{s}*((s-a)(s-b)(s-c)+ s(s-b)^2) \)
\( CS^2 = r^2 + CY^2 = r^2 + (s-c)^2 = \frac{1}{s}*((s-a)(s-b)(s-c)+ s(s-c)^2) \)