Bestimmen Sie die allgemeine Lösung folgender DGL mit dem Lösungsansatz y(x)=e^(λx) , λeℂ

Question

Aufgabe:

Bestimmen Sie die allgemeine Lösung folgender DGL mit dem Lösungsansatz y(x)=e^(λx) , λeℂ

y"-7y'+12y=0

Problem/Ansatz:

Ich wäre für jeden Ansatz, jede Lösung sehr dankbar. Ist für meine Prüfung und deshalb sehr wichtig. Ich komme leider kaum weit.

gerne auch upload anschauen, Format etwas hässlich hier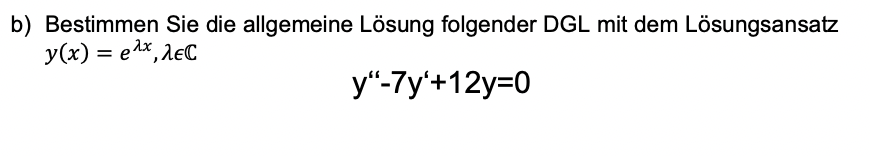

Text erkannt:

b) Bestimmen Sie die allgemeine Lösung folgender DGL mit dem Lösungsansatz \( y(x)=e^{\lambda x}, \lambda \in \mathbb{C} \)
\( y^{\prime \prime}-7 y^{\prime}+12 y=0 \)

Answer 1

Hallo

du hast doch den Ansatz? \( y(x)=e^{\lambda x}, \lambda \in \mathbb{C} \)

leite 2 mal ab, setze in die Dgl ein teile durch e^λx und löse die quadratische Gleichung für λ

die allgemeine Lösung ist dann y=C₁e^λ1x+C₂e^λ2x

lul

Answer 2

(Zu den reellen Werten): Du kannst das charakteristische Polynom durch die Gleichung bestimmen:

x^2-7x+12=0

Damit kannst du die Nullstellen mittels pq-Formel bestimmen, habe raus: x1=3 und x2=4

Mit den Nullstellen als Lamda-Werte kannst du dann ein Paar der Lösungen bestimmen.