Die Aufgabe bezieht sich auf das Thema der Warteschlangenformel / Pooling (aus dem Supply Chain Management).
Hier werden statt einem Bearbeiter eines Mailkorbs, die Kapazitäten erhöht und 2 Bearbeiter (siehe m) eingesetzt um den Prozessdurchlauf im Allgemeinen zu erhöhen. (Einfluss auf Wartezeit, DLZ usw.) Die Aufgabe ist keine klassische Textaufgabe, deshalb kann ich den Angabentext leider nicht liefern.
CV ist der Variationskoeffizient (Standardabweichung dividiert durch Mittelwert) CVp ist die Variabilität der Bearbeitungszeit. Die Bearbeitungszeiten und die Verteilung der Ankunftsminuten finden sich auf dem angefügten Bild. Daraus wurden Standardabw. und Mittelwert errechnet.
CVa ist hierbei immer 1 (für die exponentialverteilten Zwischenankunftszeiten)
Lösen möchte ich, inwieweit sich der Durchlauf verschnellert, wenn man mehr Mitarbeiter einsetzt. Hier ist die Wartezeit zu berechnen, welche ich für die weiteren Berechnungen brauche.
Die weiteren Formeln bzw. Abbildungen finden sich im Ursprungspost.
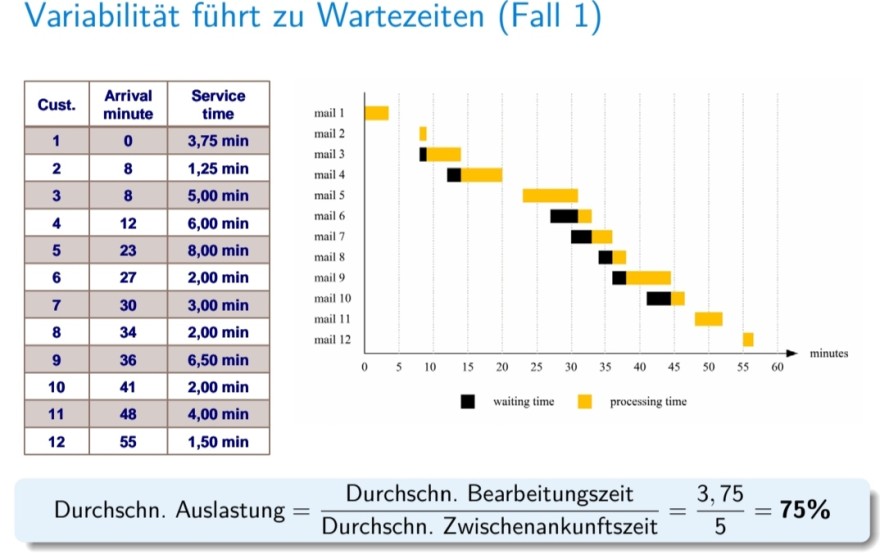
Text erkannt:
Variabilität führt zu Wartezeiten (Fall 1)
\begin{tabular}{|c|c|c|}
\hline Cust. & Arrival minute & Service time \\
\hline 1 & 0 & \( 3,75 \mathrm{~min} \) \\
\hline 2 & 8 & \( 1,25 \mathrm{~min} \) \\
\hline 3 & 8 & \( 5,00 \mathrm{~min} \) \\
\hline 4 & 12 & \( 6,00 \mathrm{~min} \) \\
\hline 5 & 23 & \( 8,00 \mathrm{~min} \) \\
\hline 6 & 27 & \( 2,00 \mathrm{~min} \) \\
\hline 7 & 30 & \( 3,00 \mathrm{~min} \) \\
\hline 8 & 34 & \( 2,00 \mathrm{~min} \) \\
\hline 9 & 36 & \( 6,50 \mathrm{~min} \) \\
\hline 10 & 41 & \( 2,00 \mathrm{~min} \) \\
\hline 11 & 48 & \( 4,00 \mathrm{~min} \) \\
\hline 12 & 55 & \( 1,50 \mathrm{~min} \) \\
\hline
\end{tabular}
Durchschn. Auslastung \( =\frac{\text { Durchschn. Bearbeitungszeit }}{\text { Durchschn. Zwischenankunftszeit }}=\frac{3,75}{5}=75 \% \)
Ich brauche bitte Eure Hilfe. Ich kann folgende Gleichung trotz vorhandenem Lösungsweg und Ergebnis nicht lösen. (2 Beispiele angefügt) Ich denke, dass ich beim mittleren Schritt einen Fehler mache, wo es um die Wurzel geht und ich diese falsch auflöse bzw. berechne. (Auslastung)