ZUerst Hier Beweis Teil KOKMPLET:

Text erkannt:
Information (1) Satz über Winkel im Sehnenviereck - Beweis
Wir uberprüfen nun die obige Vermutung durch einen Beweis.
Voraussetzung (wir wissen):
Das Viereck ABCD ist ein Sehnenviereck, d.h. die Eckpunkte A, B. C und D liegen auf einem Kreis um einen Punkt M.
Behauptung (wir wollen zeigen):
\( \alpha+\gamma=180^{\circ} \) und \( \beta+\delta=180^{\circ} \)
Beweis:
Zum Beweis verbinden wir den Mittelpunkt des Umkreises mitden vier Eckpunkten A, B, C und D.
Die Dreiecke ABM, BCM, CDM und DAM sind gleichschenklig, weil die Seiten \( \overline{\mathrm{MA}}, \overline{\mathrm{MB}}, \overline{\mathrm{MC}} \) Basiswinkel- satz fur
\( \begin{array}{l}\text { Satz für } \\ \text { gleichscherklige }\end{array} \quad \alpha_{1}=\beta_{1} ; \quad \beta_{2}=\gamma_{2} ; \quad \gamma_{1}=\delta_{1} ; \quad \delta_{2}=\alpha_{2} \),
weil sie jeweils Basiswinkel in den gleichschenkligen Dreiecken sind.
Durch die Zerlegung des Sehnenvierecks in Dreiecke sind an den Eckpunkten insgesam 8 Wirkel entstanden. Farbt man gleich große Winkel mit derselben Farbe, so benötigt man vier Faben.
Wir erkennen nun: In den zwei gegenubberliegenden Winkeln \( \alpha \) und y kommen alle vier Farben vor ebenso in den gegenüberliegenden Winkeln \( \beta \) und \( \delta \). Also:
\( \alpha+\gamma=\beta+\delta \)
Wir können dies auch rechnerisch überprüfen:
\( \alpha+\gamma=\alpha_{1}+\alpha_{2}+\gamma_{1}+\gamma_{2} \)
\( =\beta_{1}+\delta_{2}+\delta_{1}+\beta_{2} \), da wie oben gezeigt: \( \quad \alpha_{1}=\beta_{1} ; \quad \alpha_{2}=\delta_{2}: \quad \gamma_{1}=\delta_{1}: \quad \gamma_{2}=\beta_{2} \)
\( =\beta_{1}+\beta_{2}+\delta_{1}+\delta_{2} \)
\( =\beta+\delta \)
Weiter Beweis Teil 1( Inerhalb)
Text erkannt:
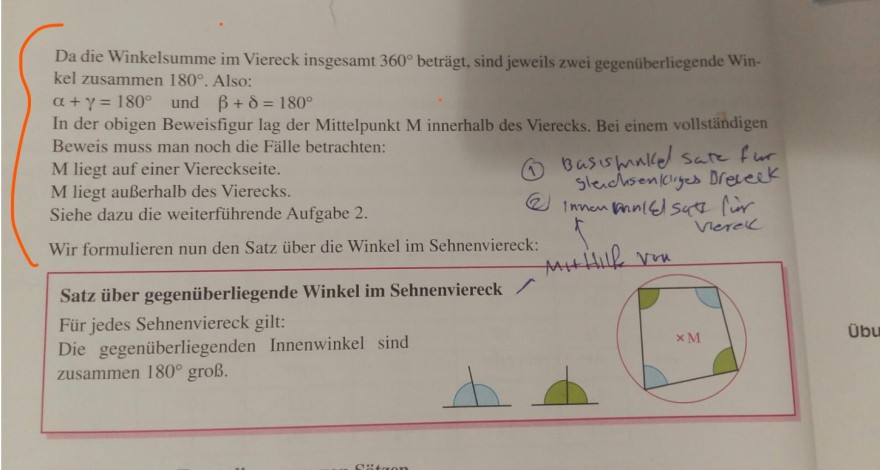
Da die Winkelsumme im Viereck insgesamt \( 360^{\circ} \) beträgt, sind jeweils zwei gegenüberliegende Winkel zusammen \( 180^{\circ} \). Also:
\( \alpha+\gamma=180^{\circ} \) und \( \beta+\delta=180^{\circ} \)
In der obigen Beweisfigur lag der Mittelpunkt \( \mathrm{M} \) innerhalb des Vierecks. Bei einem vollständigen Beweis muss man noch die Fälle betrachten:
M liegt auf einer Viereckseite.
M liegt außerhalb des Vierecks.
(1) Busushnlel sate fur
Siehe dazu die weiterführende Aufgabe \( 2 . \)
(2) innon ann(e) sut fir
Wir formulieren nun den Satz über die Winkel im Sehnenviereck:
Satz über gegenüberliegende Winkel im Sehnenviereck
Für jedes Sehnenviereck gilt:
Die gegenüberliegenden Innenwinkel sind zusammen \( 180^{\circ} \) groß.
Jetzt Beweis Teil 2( Ausserhalb)
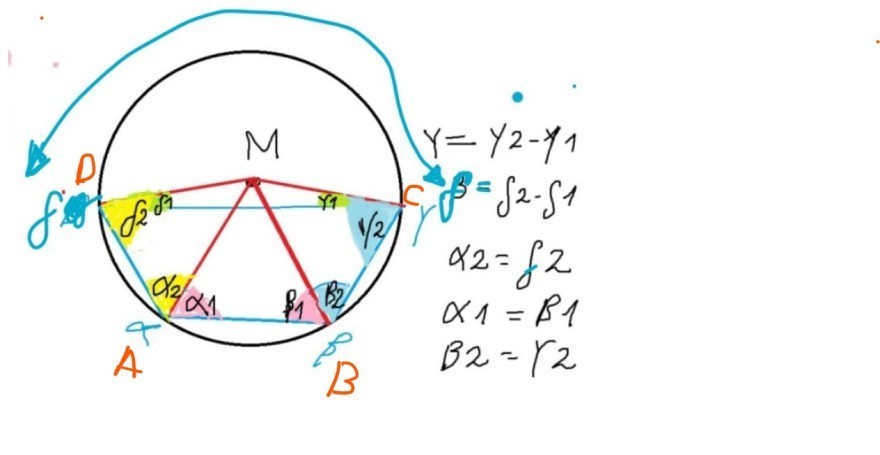
Jetzt der Beweis Teil 2 (Mittelpunkt außerhalb des Vierecks):
Das Viereck ABCD ist ein Sehnenviereck, d.h. die Eckpunkte A. B. C und D liegen auf einem Kreis um einen Punkt M.
Behauptung (wir wollen zeigen): α+γ=180 und β+δ=180
und γ= y2-γ1 und δ= δ2-δ1
Beweis: Zum Beweis verbinden wir den Mittelpunkt des Umkreises mit den vier Eckpunkten A, B, C und D.
Die Dreiecke ABM, BCM, CDM und DAM sind gleichschenklig, weil die Seiten MA, MB, MC und MD Radien des Umkreises und damit gleich lang ..
Es gilt:
α1= β1 , β2=y2 , α2= δ2 , y1= δ1
Durch die Zerlegung des Sehnenvierecks in Dreiecke sind an den Eckpunkten insgesamt 8 Winkel entstanden. Färbt man gleich große Winkel mit derselben Farbe, so benötigt man VIER Farben((( lila,gelb,blau, grün)).Wir erkennen nun: In den zwei gegenüberliegenden Winkeln α und y kommen alle VIER Farben vor ebenso bei β und δ
α+y =β+δ
(( hier habe ich viel überlegt und konnte e sehr schwer konzentrieren, habe so geblieben m bis es mir gelungen hat))
also
α+y =β+δ
Wir können das rechnerisch prüfen.(( wir wissen schon α1=β1 ; α2=δ2 ; β2=y2 ;
y=y2-1 ; δ=δ2-δ1 ; y1=δ1
α+y =α1+α2+(y)
α+y =α1+α2+(y2-y1)
α+y =α1+α2+(y2-y1)
α+y =β1+δ2+(y2-δ1)
α+y =β1+δ2+((y2))-δ1
α+y =β1+δ2+((β2))-δ1
α+y =β1+((β2))+ δ2-δ1
α+y ={{β1+β2}} + [[δ2-δ1]]
α+y ={{β}} + [[δ]]
α+y =β+ δ
da die Winkelsumme im Viereck insgesamt haben 360 beträgt sind die weil zwei gegenüberliegende Winkel zusammen 180
also --> α+y= 180 und β+ δ=180
stimmt alles