Wie sieht R aufgezeichnet aus in Teilaufgabe 4)?

Question

Aufgabe: Zeichne R ={x+iy ∈ CI x,y ∈ Z}

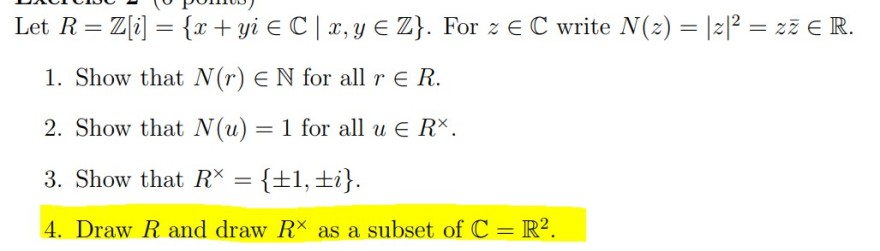
Text erkannt:

Let \( R=\mathbb{Z}[i]=\{x+y i \in \mathbb{C} \mid x, y \in \mathbb{Z}\} \). For \( z \in \mathbb{C} \) write \( N(z)=|z|^{2}=z \bar{z} \in \mathbb{R} \).
1. Show that \( N(r) \in \mathbb{N} \) for all \( r \in R \).
2. Show that \( N(u)=1 \) for all \( u \in R^{\times} \).
3. Show that \( R^{\times}=\{ \pm 1, \pm i\} \).
4. Draw \( R \) and draw \( R^{\times} \)as a subset of \( \mathbb{C}=\mathbb{R}^{2} \).

Problem/Ansatz:

Wie soll ich R aufzeichnen können? Habe nicht mal einen Ansatz

Comments

hast du dir überleg ein Koordinatensystem mit Imaginär und Realteil als Achsen zu zeichnen? Dann kannst du das ziemlich einfach einzeichnen

Answer 1

Draw \( R \) and draw \( R^{\times} \)as a subset of \( \mathbb{C}=\mathbb{R}^{2} \).

Answer 2

Hallo

es sind einfach die ganzzahlen Punkte  also z.B(2,3) (-4,5) (-2,-3) usw. für R

Allerdings weiss ich nicht was die R^x ist?

lul