Flächeninhalt Trapez durch Teildreiecke

Question

Aufgabe:

Text erkannt:

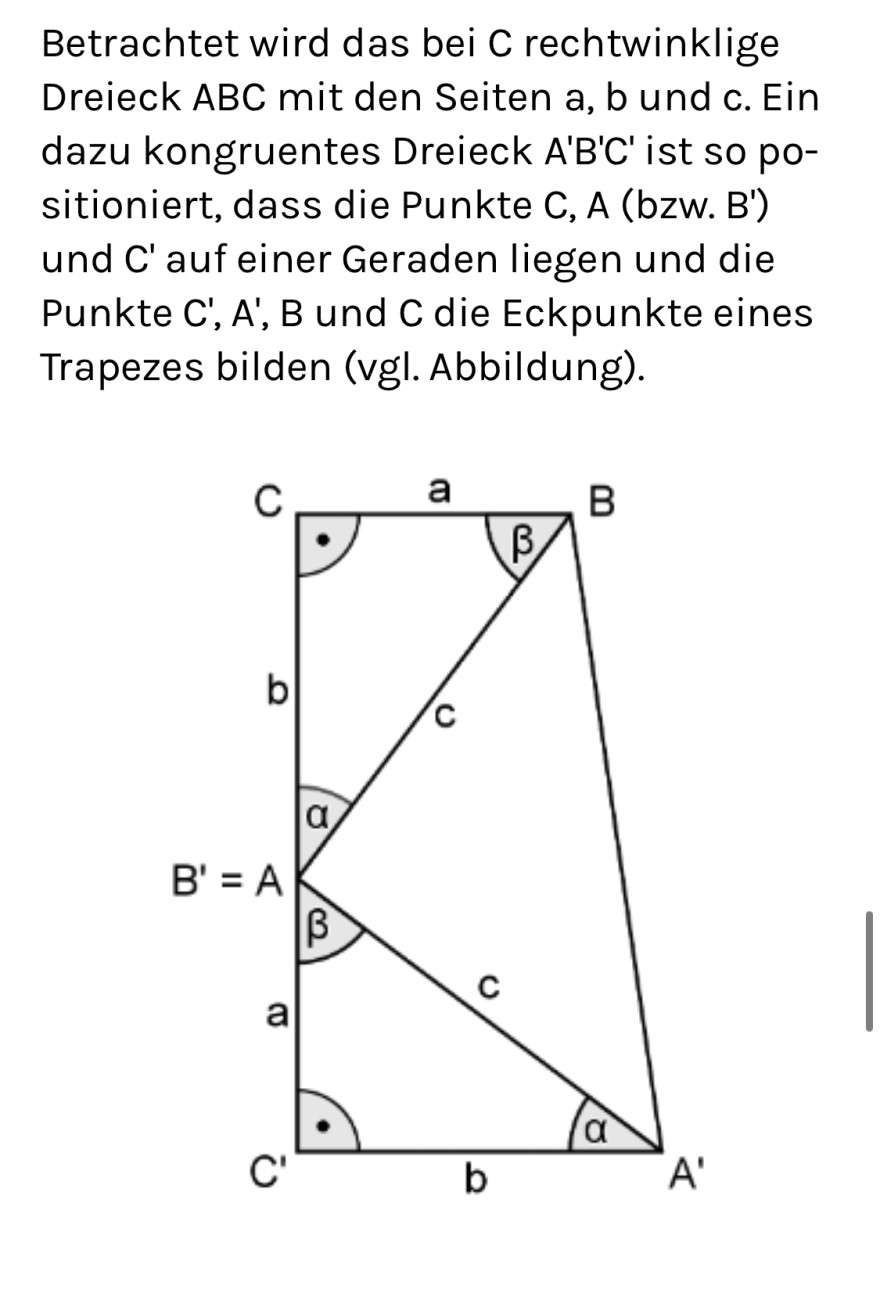
Der Flächeninhalt des Trapezes C'A'BC kann sowohl mit dem Term \( \frac{1}{2} \cdot(a+b) \). \( (a+b) \) berechnet werden, der sich unmittelbar aus der bekannten „Trapezformel" ergibt, als auch mit einem Term, der sich aus der Betrachtung der Teildreiecke des Trapezes ergibt. Übersetzen Sie diese Informationen in eine Gleichung und folgern Sie hieraus sie Beziehung \( a^{2}+ \) \( b^{2}=c^{2} \)

Die Lösung der Aufgabe:

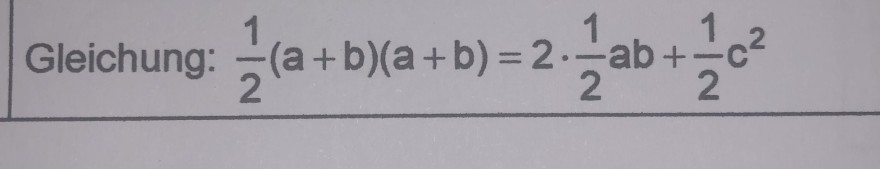
Text erkannt:

Gleichung: \( \frac{1}{2}(a+b)(a+b)=2 \cdot \frac{1}{2} a b+\frac{1}{2} c^{2} \)

Problem:
Ich kann hier leider nicht nachvollziehen, wie man auf 1/2 • \( c^{2} \) kommt, könnte mir das jemand vielleicht erklären. Normalerweise wird der Flächeninhalt des 3. Dreiecks mit 1/2 •c•h ausgerechnet, jedoch steht es in der Lösung anders

Answer 1

Das 3. Teildreieck ist rechtwinklig mit den

Katheten, die beide die Länge c haben, also

Fläche c^2 / 2.

Comments

Ich dachte man rechnet den Flächeninhalt eines Rechtwinkligen Dreiecks mit 1/2 • Basis• Höhe. Warum kann man hier die 2 Katheten durch 2 teilen und dann hat man den Flächeninhalt?

---

Wenn man eine Kathete als Grundseite nimmt,

ist die andere die zugehörige Höhe.