Hallo,
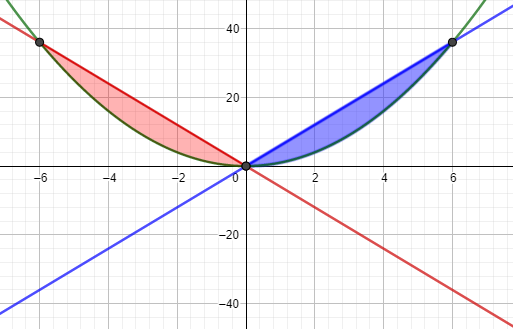
eine Gerade durch den Ursprung hat die Form y = mx
Den Flächeninhalt zwischen zwei Graphen berechnest du, indem du zunächst die Schnittpunkte bestimmst. Dazu werden die Funktionsgleichungen gleichgesetzt.
\(x^2=mx\)
\(x^2-mx=0\\ x\cdot (x-m)=0\\x_1=0\quad \quad x_2 = m\)
In der 2. Gleichung ist auf der linken Seite die Differenzfunktion. Davon bildest du die Stammfunktion:
\(F(x)=\frac{1}{3}x^3-\frac{1}{2}mx^2\)
Jetzt die Berechnung des Integrals:
\( \int \limits_{0}^{m}\left(x^{2}-m x\right) d x=\left|\left[\frac{1}{3} x^{3}-\frac{1}{2} m x^{2}\right]_{0}^{m}\right| \)
\( =\left|\frac{1}{3} m^{3}-\frac{1}{2} m^{3}\right|=\left|-\frac{1}{6}m^3\right|=\frac{1}{6} m^{3} \)
Da du den Flächeninhalt kennst, musst du nur noch nach m auflösen:
\( \frac{1}{6} m^{3}=36 \)
m = 6 für m > 0 und m = -6 für m < 0
Gruß, Silvia