Ich habe in der Schule folgende Aufgabe gekriegt:
Es sei ein konvexes Fünfeck ABCDE und u die Summe der Seitenlängen (Also der Umfang). d sei die Summe der Diagonalenlängen.
a) Zeige dass stets d<2u gilt.
b) Zeige dass stets u<d gilt.
Mein Ansatz für b) war folgender:
# b)
Als erstes Beschriften wir alle Seiten und diagonalen im Fünfeck. Die Seiten mit den Namen \(S_a\), \(S_b\), \(S_c\), \(S_d\) und \(S_e\) und den Diagonalen mit den Namen \(D_a\), \(D_b\), \(D_c\), \(D_d\) und \(D_e\).
Jetzt ordnen wir jeder \(S\) eine \(D\) zu (die mit dem gleichen Buchstaben). Da wir uns in einem Konvexem Fünfeck befinden ist jede zugeordnete \(D\) länger als die entsprechende \(S\), da sie über die andere \(S\) herausreicht. Dies kann man in meiner Skizze sehen. Es funktioniert bei allen Fünfecken.<
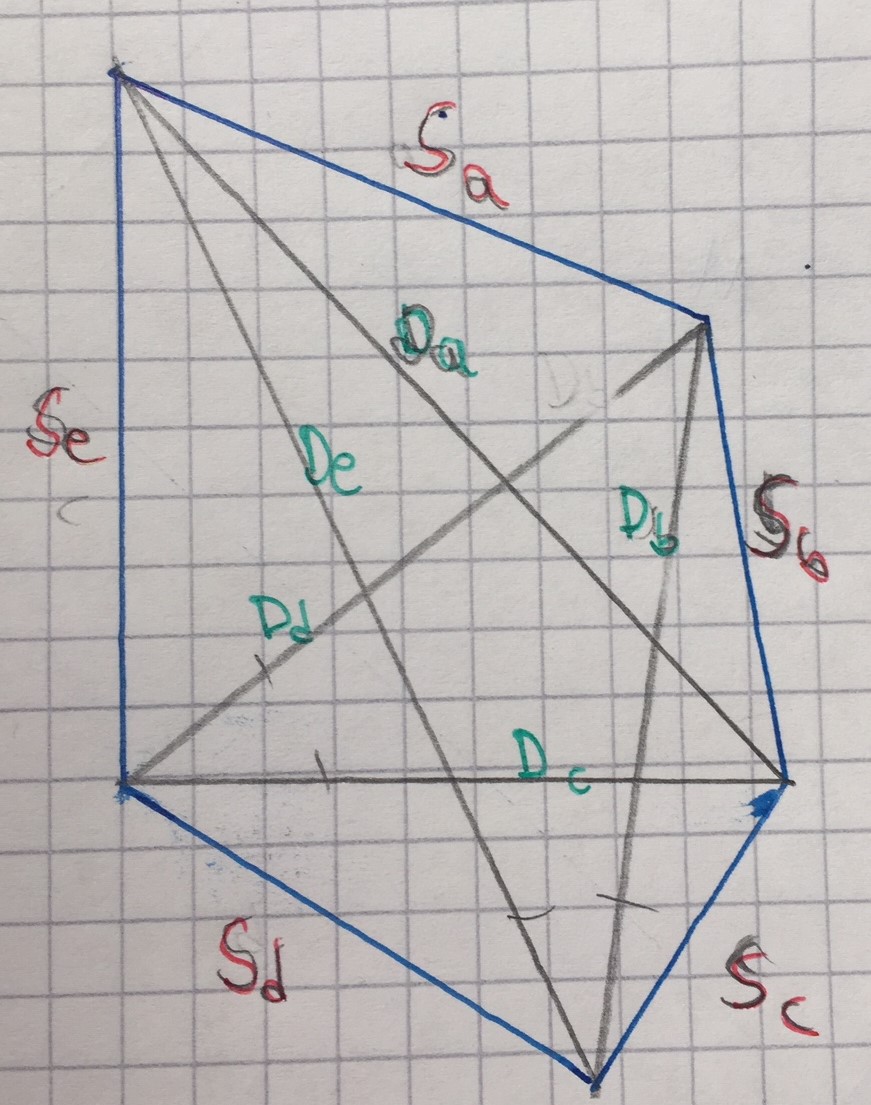
.
Ich bin mir allerdings noch nicht sicher ob das der richtige Ansatz ist. Für a) habe ich noch gar keinen Ansatz. Könnte mir jemand helfen?
Vielen Dank im Voraus :)