Wie viele Möglichkeiten gibt es, aus einer Klasse mit 20 Schülern eine Lerngruppe zu bilden, die mindestens eine …

Question

Aufgabe:

Wie viele Möglichkeiten gibt es, aus einer Klasse mit 20 Schülern eine Lerngruppe zu bilden, die mindestens eine Person von den 3 Strebern Tom, Sophia und Lynn enthält? Eine Lerngruppe besteht aus mindestens 2 Schülern.

Problem/Ansatz:

Betrachten wir erstmal eine Gruppe die nur aus 2 Schülern besteht.

Ein Streber kann mit 17 Schülern in einer Zweiergruppe sein. 3x17 = 51
Oder 2 Streber können in einer Zweiergruppe sein. Dann 3!/2!1! = 3

Dann eine Gruppe mit 3 Schüler und einem Streber: 17!/2!15! = 136

Und hier stelle ich mir die Frage ob es nicht einen einfacheren Weg gibt.

Answer 1

Ich würde eine Fallunterscheidung in zwei Fälle machen

Du nimmst eine Person von den Strebern und mind. eine weitere vom Rest.

393213 Möglichkeiten

Du nimmst mind. 2 Personen von den Strebern und beliebig viele vom Rest.

524288 Möglichkeiten

Ich komme damit auf 917501 Möglichkeiten. Also etwas weniger als 'ne Million.

Meist du ich habe deine Forderungen richtig verstanden. Dann könntest du mal Probieren ob du auf ähnliche Werte kommst.

Comments

Meist du ich habe deine Forderungen richtig verstanden

Nein, Sie haben mich nicht richtig verstanden. Haben Sie sich überhaupt meinen Ansatz durchgelesen? Ich habe das Ergebnis doch noch mal 3 gerechnet, weil die Streber unterscheidbar sind.

Aber selbst wenn man Ihr Ergebnis mit 3 multipliziert kommt das falsche Ergebnis raus.

Ich bin den schlaueren Weg gegangen, nämlich über die Gegenmöglichkeit.
Mit Wolfram: sum from x=2 to 20 of x!/(2!(x-2)!) - sum from x=2 to 17 of x!/(2!(x-2)!) bis 17 hoch.

Hier sind alle Werte in einer Tabelle:

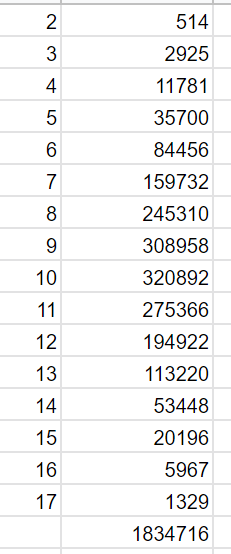
A: Es gibt insgesamt 1.834.716 Möglichkeiten eine Lerngruppe zu bilden, die mindestens eine von den 3 Strebern enthält.

Wie kommen Sie überhaupt auf diese Zahlen? Und wollten Sie eigentlich nicht erst prüfen ob das richtig ist, was Sie in diesem Forum schreiben?

P.S.: Plus die Möglichkeiten mit mindestens ein Streber in einer 18er, 19er, 20er Gruppe noch.

---

Ein Streber kann mit 17 Schülern in einer Zweiergruppe sein. 3x17 = 51
Oder 2 Streber können in einer Zweiergruppe sein. Dann 3!/2!1! = 3

Der Ansatz ist schon richtig. Das sind insgesamt 54 Möglichkeiten. Und sollte ich die 54 nicht jetzt auch für die 2er Gruppe in der Tabelle finden oder wie ist die Tabelle gemeint? Dort stehen hinter der 2 ja 514?

Richtig wäre hier

binomial(20,2)-binomial(17,2) = 54 mit wolfram alpha

https://www.wolframalpha.com/input?i=binomial%2820%2C2%29-binomial%2817%2C2%29

Warum du da noch zwei Summen bildest, ist mir leider völlig schleierhaft.

Und wenn ich das jetzt summiere von 2 bis 20 komme ich auch auf meine Zahl

Denk vielleicht mal drüber nach.

---

Ich fand meine erste Berechnung aber etwas schöner. Keine Binomialkoeffizienten und keine Summe.

https://www.wolframalpha.com/input?i=3*%282%5E17-1%29%2B4*%282%5E17%29

---

Vielleicht sieht er

leichter ein

---

Was macht der Rechner mit dem 2. BKoeff für n=2 und k=3?

---

(17 über -1)  =  0

---

Ich bin den schlaueren Weg gegangen, nämlich über die Gegenmöglichkeit.

Hier strotzt aber jemand vor Selbstbewusstsein.