Hallo,
Der "Trick" besteht in dem Ausklammern von x.
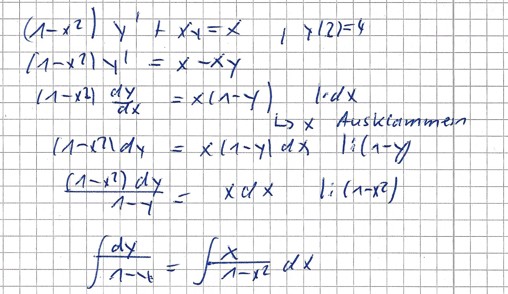

Zum Schluss noch die AWB in die Lösung einsetzen.
Lösung: \( y(x)=C_{1} \sqrt{x^{2}-1}+1 \)
da bei (1-y) dividiert wird , geht eine Lösung verloren.
-->1-y = 0 -->y=1
mit AWB : \( y(x)=\sqrt{3} \sqrt{x^{2}-1}+1 \)