Wäre nett, wenn mir hierbei mal jemand etwas weiterhelfen könnte. Sehe bei der Aufgabe grundsätzlich (z.B in Hinblick auf I und II) Fälle, wo es mal klappt und jedoch zugleich auch andere Fälle existieren, die wiederum zu einer Verletzung der Aussage führen

Text erkannt:
Aufgabe \( 2.3 \quad(3+3=6 \) Punkte \( ) \)
Seien \( a, b, c \in M \) beliebig und \( F: 2^{M} \rightarrow B \) eine injektive Funktion mit folgenden Eigenschaften:
\( \begin{array}{c} F(X) \otimes F(Y)=F(X \cup Y) \\ F(X) \diamond F(Y)=F(X \cap Y) . \end{array} \)
Wir wollen Beziehungen der Form \( a \square b \bigcirc a \square c \) betrachten, wobei \( \square \in\{=, \neq\}, \bigcirc \in \) \{und,oder \( \} \). Welche dieser Beziehungen für \( a, b, c \) folgen aus den Gleichungen und Ungleichungen über \( F \) ? Beweisen Sie Ihre Behauptungen.
a) I ) \( F(\{a\}) \neq F(\{b\}) \otimes F(\{c\}) \)
II ) \( F(\{a\})=F(\{b\}) \odot F(\{c\}) \)
b) I ) \( F(\{a\})=(F(\{b\}) \otimes F(\{c\})) \diamond F(\{a\}) \)
II ) \( F(\{a\}) \neq(F(\{b\}) \otimes F(\{c\})) \diamond F(\{a\}) \)
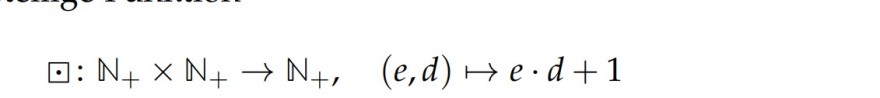
Text erkannt:
\( \odot: \mathbb{N}_{+} \times \mathbb{N}_{+} \rightarrow \mathbb{N}_{+}, \quad(e, d) \mapsto e \cdot d+1 \)