Erstellung Quadratische Funktion für Textaufgabe Schiffsbeladung/Lastkahn

Question

Aufgabe: Erstellung Funktionsgleichung auf Basis Lastkahn (Schiffsbeladung)

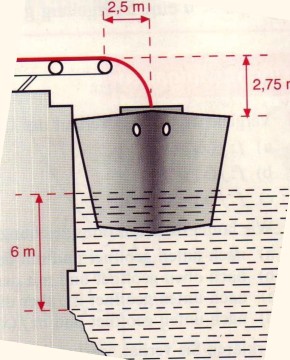
Ein Lastkahn soll über Förderbandanlage mit Sand beladen werden. Der Kahn wurde so festgemacht, dass Sandstrahl genau durch die Mitte der 4 Meter bereiter Öffnung in den Laderaum fällt. DER Sand strahl verläuft annähernd Parabelförmig. Gleich Beginn der  ladervargangs fällt das Förderbands wegen eines Mototdefekt aus. Nach einigen Stunden ist der Wasserspiegel wegen der eingetretenen Ebbe um 6 m gefallen.

Frage:

a) Begründen Sie mit einer Rechnung dass der Parabelförmig verlaufende Sandstrahl nach eingetretenen Ebbe die Ladeöffnung noch trifft.

b) Nach Beladen des Schiffs durch sein zusätzliches Gewicht um 2 Meter weiter gesunken. Weisen Sie rechnerisch nach, dass Die Öffnung nicht mehr getroffen wird und geben Sie an um wie viel Das Schiff nach rechts verschoben werden müsste.

C) Bestimmen.Sie maximale Tiefgang, so dass der Sandstrahl noch die Öffnung trifft.

Gemäss Bild Sandstrah ist 2,5 m bereit wie eine halbeparabel 2.5 m und fällt von 2,75 m hoch in die Ladeöffnung fällt.

Text erkannt:

Quelle: Anwendungsbezogene Analysis, Bildungsverlag EINS, 2004

Bild aus Duplikat ergänzt:

Answer 1

Machen wir erstmal einen Plan, Deine Angaben würde ich umsetzen wie

Entspricht das Deinen Buchangaben?

Man könnte den Scheitel der Parabel auch auf den Ursprung legen, hätte dann unübersichtlichere Einlaufstellen...

Comments

Besten Dank. Wie kann man Rechnerisch nachweisen?

---

In dem man die Funktionsgleichung der Parabel ermittelt.

Scheitel S und ein Punkt C bekannt

p(x) = a (x-S_x)²+S_y

---

Wie kann ich bei Aufgabe b) x- Werte von Punkte F (4,443/ -8) rechnerisch finden? Herzlichen Dank

---

Du mußt nachschauen welches x>0 für p(x)=-8 in Frage kommt...

---

Soll ich nach Normalform von Funktion finden?

---

Es ist rechnerisch egal in welcher Form die Parabel aufgeschrieben wird.
ggf. mußt Du die Normalform (was immer ihr darunter versteht) halt herstellen...

In Deinem Post steht davon nix!

---

Sorry, wie konntest du bei Scheitelpunkt x Werte finden. Es hat nicht gegeben.

---

>Gemäss Bild Sandstrah ist 2,5 m bereit wie eine halbeparabel 2.5 m und fällt von 2,75 m hoch in die Ladeöffnung fällt.<

Kein Bild vorhanden, ein mögliches geliefert...

---

Du hast bei Seitelpunkt für X Wert -0,5 gegeben. Wie kommst du darauf? Es ist für mich  leider nicht verständlich. Hast du eine Rechnenweg? Merci für deine Antwort.

---

Du hast bei Seitelpunkt für X Wert -0,5 gegeben. Wie kommst du darauf?

Es ist letzlich egal, wo man den Scheitelpunkt der Parabel hinlegt. Wichtig ist nur, dass der 'Einlaufpunkt' (Mitte Ladeöffnung) 2,5 horizontal und -2,75 vertikal vom Scheitelpunkt entfernt liegt.

---

Wie kann ich die b und c lösen? Es war mir nicht klar.

---

Wenn man den Scheitelpunkt in den Ursprung legt, lautet die Gleichung der Parabel$$p(x) = -0,44 x^2$$

Weisen Sie rechnerisch nach, dass Die Öffnung nicht mehr getroffen wird und geben Sie an um wie viel Das Schiff nach rechts verschoben werden müsste.

Die Ladeöffnung liegt dann bei \(y_L=-2,75-6-2=-10,75\). Und das rechte Ende der Öffnung immer noch bei \(x_L = 2,5+2=4,5\). Die X-Koordinate der Parabel ist $$p(x_8) = -0,44x_8^2 = y_L=-10,75 \\\implies x_8 = \sqrt{\frac{-10,75}{-0,44}} \approx 4,9 \gt 4,5 = x_L$$also rechts von der Ladeöffnung. Die Verschiebung zu berechnen sollte kein Problem sein.

Hier noch mal eine Skizze, die das verdeutlicht:

C) Bestimmen.Sie maximale Tiefgang, so dass der Sandstrahl noch die Öffnung trifft.

Bestimme den Y-Wert für \(p(x_L)\) und dann schließe daraus auf den Tiefgang.

---

Wie kann ich die b und c lösen? Es war mir nicht klar.

Besten Dank für diese ausführliche Lösungsvorschlag. Weshalb bei dem Grafik Koordinatensystem der Punkt 4.9 für berechnete X Wert nah so Ursprung als Punkt 4.5 liegt. Normalerweise soll es auf Koordinatensystem 4.5/ 10.75 und dann unten 4.9/ 10.75 sein, oder?

---

Es war mir nicht klar.

Dann stelle bitte konkrete Fagen. WAS ist nicht klar?

Weshalb bei dem Grafik Koordinatensystem der Punkt 4.9 für berechnete X Wert nah so Ursprung als Punkt 4.5 liegt.

Weil die Aufgabenstellung so ist, wie sie ist.

Normalerweise soll es auf Koordinatensystem 4.5/ 10.75 und dann unten 4.9/ 10.75 sein, oder?

Der linke Punkt ist \((x_L=4,5|\,-10,75)\) und

der rechte ist \((x_8=4,943|\,-10,75)\). Der Text zu den Punkten ist wohl verrutscht.