Aufgabe:
Aus drei Brettern der Breite g soll ein Kanal mit maxi- malem Fassungsvermögen gebaut werden. Hierfür muss der Flächeninhalt Q des trapezförmigen Querschnittes des Kanals maximiert werden (vgl. Skizze).
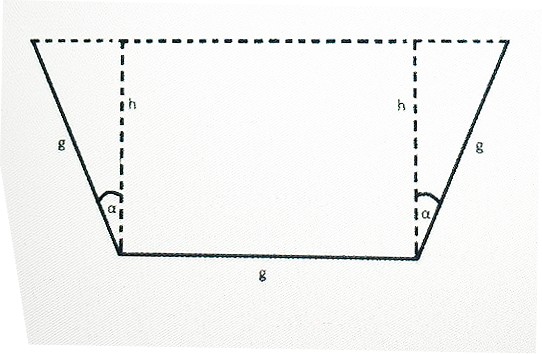
Wie muss der Winkel α (in der Skizze) gewählt werden, damit der Flächeninahlt Q maximal wird?
Gehen Sie zur Lösung des Problems wie folgt vor:
(i) Begründen Sie, dass der Flächeninhalt Q (mit den Bezeichnungen aus der Skizze) gegeben ist durch Q = gh(1 + sin(α)).
(ii) Beschreiben Sie Q als Funktion einer Variablen, indem Sie die Höhe h in Abhängigkeit des Winkels α ausdrücken und überlegen Sie sich einen geeigneten Parameterbereich für α.
(iii) Führen Sie die notwendige Bedingung für ein Maximum (im Inneren des Parameterbereiches) auf die Gleichung 2x2 + x − 1 = 0 mit x = sin(α) zurück und lösen Sie diese unter den gegebenen Nebenbedingungen.
(iv) Aus Teil (iii) erhalten Sie als einzigen Kandidaten den Winkel α = π6 . Überprüfen Sie, ob es sich hierbei tatsächlich um die Lösung des gegebenen Maximierungsproblems handelt und bestimmen Sie den maximalen Flächeninhalt für Q.
Problem/Ansatz:
Kann mir jemand dabei helfen ?