Zeigen Sie, dass sich unabhängig der Turmhöhe das Optimum einstellt, wenn die Winkel (zwischen Seil

Question

Aufgabe:

Sie haben zwei Sendemasten. Der eine ist 5m hoch der andere 3m. Beide Masten stehen
15m voneinander entfernt und sollen durch ein Seil am Boden gesichert werden. Dazu geht ein Seil von der
Spitze eines Mastes zum Anker A am Boden.
a) Wo muss A liegen, damit Gesamtlänge der beiden Seile minimal wird?
Tipp: Quadratzahlen, die Niemand kennt: 75² = 5625.
b) Zeigen Sie, dass sich unabhängig der Turmhöhe das Optimum einstellt, wenn die Winkel (zwischen Seil
und Boden) bei A gleich sind.

Problem/Ansatz:

Hallo, ich habe bei a) bereits eine Idee, die zu einer Lösung führt. Unzwar habe ich die 15m in 3/5 und 2/5 entsprechend dem Verhältnis der Höhen beider Masten aufgeteilt. Das Problem ist allerdings, das ich das ganze Modelliert habe und dabei eine vermeintlich optimalere Lösung entsprechend der Aufgabe b) heraus kommt. Hier mal das Modell:

Jetzt habe ich gleich das nächste Problem. Wie finde ich da einen Ansatz, bei dem ich die optimale Lösung auf die gleichen Winkel reduzieren kann?

Über Hilfe würde ich mich sehr freuen.

Comments

Wenn du Differentialrechnung schon kennst
kann damit alles exakt ausgerechnet werden.

Bin bei Bedarf gern weiter behilflich.

mfg Georg

Answer 1

y = 5 - 8/15·x = 0 --> x = 9.375 m

Der optimale Ankerpunkt befindet sich 9.375 m vom ersten Mast entfernt.

Comments

Danke für die schnelle Antwort. Das deckt sich ja auch so weit mit meinem Modell. Allerdings kann ich nicht so ganz nachvollziehen, woher die 8/15 kommen.

---

Steigung zwischen dem Punkt (0 | 5) und dem Punkt (15 | -3).

---

Ok, das ergibt Sinn. Vielen Dank.

Hast du eine Idee, wie ich bei b Argumentieren kann?

Meine Idee ist bis jetzt, dass ich bei gleichen Winkeln die Hypotenuse am kleinsten ist. Jedoch kann ich das nicht mathematisch formulieren. Ist das überhaupt richtig?

Meine Überlegung war, das ja wenn eine Hypotenuse sehr klein wird die andere dafür um so größer und deshalb es mehr Seil benötigt.

---

Bei der Spiegelung des zweiten Sendemastes nach unten ergibt sich beim Schitt der zwei Geraden Scheitelwinkel die natürlich gleich groß sind.

Answer 2

"a) Wo muss A liegen, damit Gesamtlänge der beiden Seile minimal wird?"

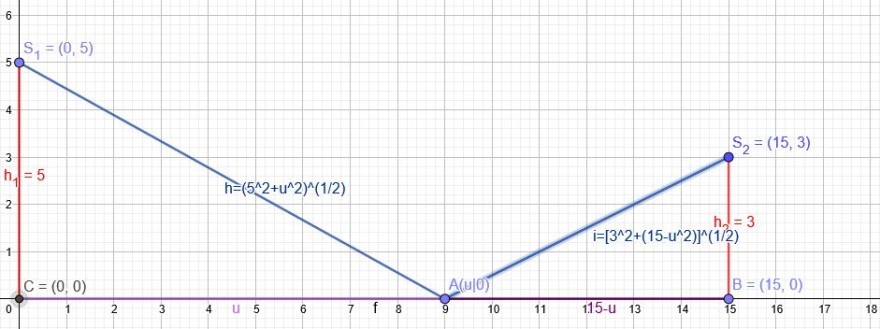
\(l(u)= \sqrt{5^2+u^2}+\sqrt{3^2+(15-u)^2} \) soll minimal werden.

\(l(u)= \sqrt{25+u^2}+\sqrt{234-30u+u^2} \)

\(l´(u)= \frac{2u}{2*\sqrt{25+u^2}}+\frac{2u-30}{2*\sqrt{234-30u+u^2}}\)

\(l´(u)= \frac{u}{\sqrt{25+u^2}}+\frac{u-15}{\sqrt{234-30u+u^2}}\)

\( \frac{u}{\sqrt{25+u^2}}+\frac{u-15}{\sqrt{234-30u+u^2}}=0\)

\( \frac{u}{\sqrt{25+u^2}}=\frac{15-u}{\sqrt{234-30u+u^2}}     |^{2}\)

\( \frac{u^2}{25+u^2}=\frac{225-30u+u^2}{234-30u+u^2}   \)

\( u^{2}*(234-30u+u^2)=(25+u^{2})*(225-30u+u^2) \)

\( u_1=\frac{75}{8} \)

\( u_2=\frac{75}{2} \) kommt nicht in Betracht, weil außerhalb der Masten.