Aufgabe:
Folgende gemeinsame Wahrscheinlichkeitsverteilung der beiden Zufallsvariablen X und Y sei gegeben:
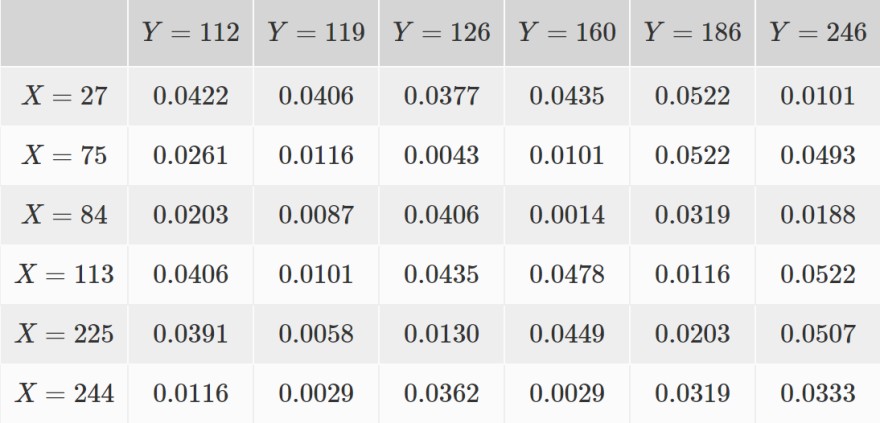
Text erkannt:
\begin{tabular}{|l|l|l|l|l|l|l|}
\hline & \( Y=112 \) & \( Y=119 \) & \( Y=126 \) & \( Y=160 \) & \( Y=186 \) & \( Y=246 \) \\
\hline\( X=27 \) & \( 0.0422 \) & \( 0.0406 \) & \( 0.0377 \) & \( 0.0435 \) & \( 0.0522 \) & \( 0.0101 \) \\
\hline\( X=75 \) & \( 0.0261 \) & \( 0.0116 \) & \( 0.0043 \) & \( 0.0101 \) & \( 0.0522 \) & \( 0.0493 \) \\
\hline\( X=84 \) & \( 0.0203 \) & \( 0.0087 \) & \( 0.0406 \) & \( 0.0014 \) & \( 0.0319 \) & \( 0.0188 \) \\
\hline\( X=113 \) & \( 0.0406 \) & \( 0.0101 \) & \( 0.0435 \) & \( 0.0478 \) & \( 0.0116 \) & \( 0.0522 \) \\
\hline\( X=225 \) & \( 0.0391 \) & \( 0.0058 \) & \( 0.0130 \) & \( 0.0449 \) & \( 0.0203 \) & \( 0.0507 \) \\
\hline\( X=244 \) & \( 0.0116 \) & \( 0.0029 \) & \( 0.0362 \) & \( 0.0029 \) & \( 0.0319 \) & \( 0.0333 \) \\
\hline
\end{tabular}
Problem/Ansatz:
Bestimmen Sie den Erwartungswert E(X|Y = 112)! Eingabe auf 4 Nachkommastellen gerundet.
Wie finde ich den erforderlichen Wert?