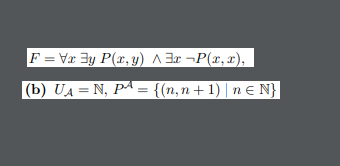
Text erkannt:
\( F=\forall x \exists y P(x, y) \wedge \exists x \neg P(x, x), \)
(b) \( U_{\mathcal{A}}=\mathbb{N}, P^{\mathcal{A}}=\{(n, n+1) \mid n \in \mathbb{N}\} \)
Hallo, ich habe eine kleine Verständnisfrage zu First-order-logic.
Kann die zweite Formel in F zu 1 evaluieren? Es existiert keine Zahl x sodass die Bedingung von P nicht erfüllt wird.
Wählen wir also ein beliebiges x, dann setzen wir x in P ein und bekommen dann die Menge (x,x+1), welche offensichtlich die Bedingung von P erfüllt da wir uns nur in den natürlichen Zahlen bewegen. Damit der zweite Teil aber wahr wird muss man ja ein x finden für das P eben nicht gilt, da dies ja danach negiert wird.
Hat jemand einen Tipp?
LG David