Begründen Sie die Richtigkeit Ihrer Konstruktion, d.h.

Question

a) Konstruieren Sie einen Kreis durch drei gegebene (verschiedene) Punkte A, B und C, und beschreiben Sie die Schritte der Konstruktion. Sie dürfen dabei die in Vorlesung und Übung verwendeten Standardkonstruktionen voraussetzen.
b) Unter welchen Bedingungen ist sichergestellt, dass die Konstruktion und ihre einzelnen Schritte aus a) durchführbar sind?
c) Begründen Sie die Richtigkeit Ihrer Konstruktion, d.h. dass tatsächlich alle drei Punkte auf dem konstruierten Kreis liegen

Answer 1

dafür bietet sich wieder Geogebra an.

Die Werkzeuge sind "Strecke", "Mittelsenkrechte" und "Kreise".

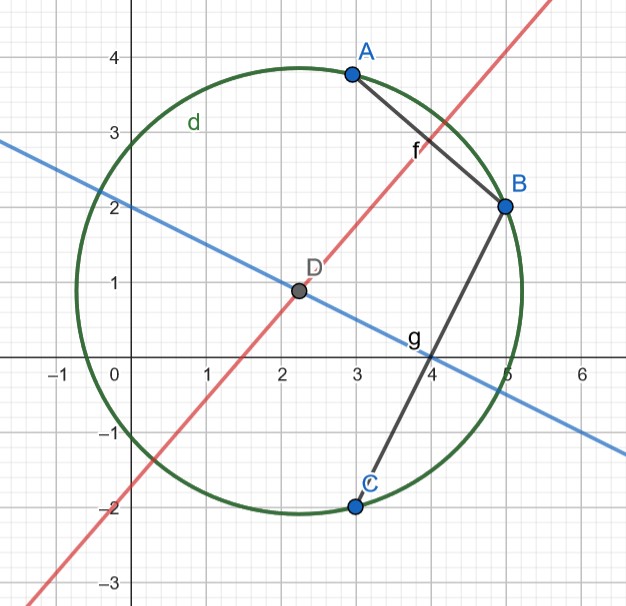
Es werden zwei Strecken benötigt, wobei die Strecken einen gemeinsam Punkt haben müssen. Dann die Mittelsenkrechten der Strecken konstruieren. Der Schnittpunkt der beiden Mittelsenkrechten ist der Kreismittelpunkt.

Das funktioniert nur, wenn die drei Punkte nicht auf einer Geraden liegen.

Bei Geogebra gibt es mehrere Kreisfunktion. Wenn man "Kreis mit MP durch Punkt" und "Kreis durch 3 Punkte" anwendet, sieht man, dass beide Kreise gleich sind.

Comments

Und was könnte ich dann bei 1b dazu schreiben ?

---

die Punkte A, B und C dürfen nicht auf einer Geraden liegen, sonst wären die Mittelsenkrechten parallel und die Mittelsenkrechten würden keinen Schnittpunkt bilden.

Auch dürfen die drei Punkte jeweils verschieden seinm das ist aber eigentlich klar, alles andere wäre Haarspalterei.