Aufgabe:
Text erkannt:
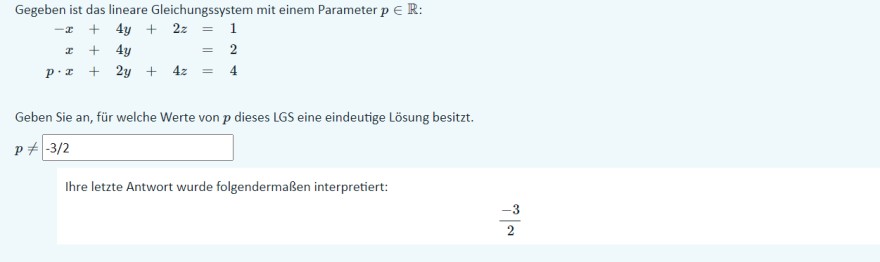
Gegeben ist das lineare Gleichungssystem mit einem Parameter \( p \in \mathbb{R} \) :
\( \begin{aligned} -x+4 y+2 z & =1 \\ x+4 y & =2 \\ p \cdot x+2 y+4 z & =4 \end{aligned} \)
Geben Sie an, für welche Werte von \( p \) dieses LGS eine eindeutige Lösung besitzt.
\( p \neq-3 / 2 \)
Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( \frac{-3}{2} \)
Problem/Ansatz:
Ich hab zuerst die Regel von Sarrus angewendet und die ersten zwei Spalten noch dazu geschrieben, dann hab ich die Determinante ausgerechnet und kam am Ende auf -8+4-8p-8 und das umgestellt etc. ist dann -3/2=p also hätte ich als Lösung p=-3/2.
Nun wollte ich fragen ob das richtig gerechnet wurde oder ob ich irgendwo einen Fehler gemacht hab.