Aufgabe:
Text erkannt:
Aufgabe \( 2(25 \mathrm{P})^{1} \)
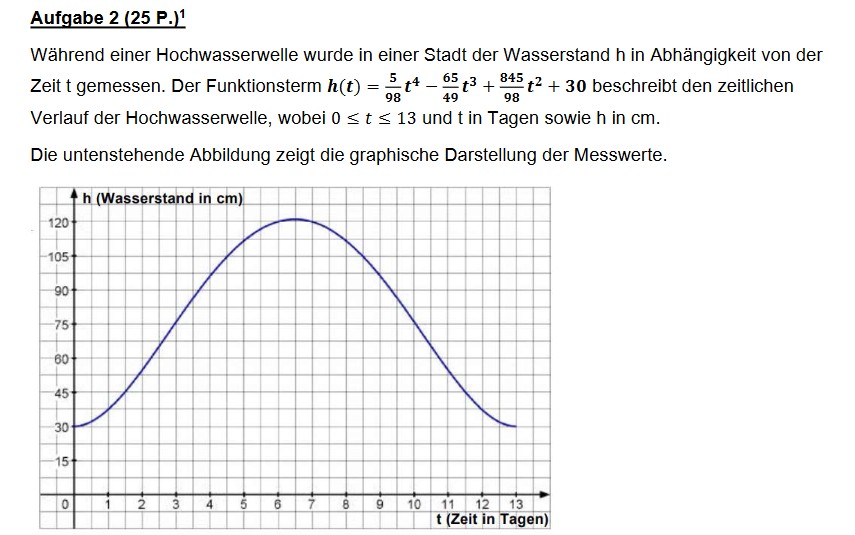
Während einer Hochwasserwelle wurde in einer Stadt der Wasserstand \( h \) in Abhängigkeit von der Zeit t gemessen. Der Funktionsterm \( h(t)=\frac{5}{98} t^{4}-\frac{65}{49} t^{3}+\frac{845}{98} t^{2}+30 \) beschreibt den zeitlichen Verlauf der Hochwasserwelle, wobei \( 0 \leq t \leq 13 \) und \( t \) in Tagen sowie \( h \) in \( \mathrm{cm} \).
Die untenstehende Abbildung zeigt die graphische Darstellung der Messwerte.
Berechnen Sie, zu welchem Zeitpunkt der Wasserstand am stärksten anstieg.
Problem/Ansatz:
Um die Aufgabe zu lösen, habe ich zunächst abgeleitet und dann h'(t) = 0 gesetzt und gelöst. Als Ergebnis erhalte ich jedoch drei mögliche Ergebnisse
t = 0 oder t = 6,5 oder t = 13
Wie lässt sich das im Zusammenhang erklären? Was hat es mit t = 0 bzw t = 13 auf sich? t = 6,5 scheint mir die gesuchte Lösung zu sein.
Eine Fragestellung später wartet noch folgende Aufgabe auf mich:
Berechnen Sie, zu welchem Zeitpunkt der höchste Wasserstand erreicht war und ermitteln
Sie, wie hoch der Wasserstand zu diesem Zeitpunkt war.
Spielt sie nicht auf das gleiche an, was ich hier bereits ausgerechnet habe? Der Zeitpunkt ist 6,5 und jetzt muss ich die 6,5 nur noch in die Funktion einsetzen, oder liege ich hier falsch? (Also h(6,5))