Guten Abend, mir erschließt sich hier leider nicht die Vorgehensweise der folgenden Aufgaben deswegen bitte ich um mögliche Lösungswege + Ansätze. Ich bedanke mich im Voraus, mfg
Zu den stärksten Quellen von Gammastrahlen in abgebrannten Brennstäben aus Kernkraftwerken gehört unter anderem Plutonium-241 (241Pu), das mit einer Halbwertszeit von 14 Jahren in Americium-241 zerfällt. Americium-241 (241Am) zerfällt seinerseits mit einer Halbwertszeit von 432 Jahren in Neptunium-237 (237Np).
(a) Wir betrachten zunächst zwei radioaktive Nuklide A und B mit Zerfallsraten
λA und λB, wobei B das Zerfallsprodukt von A sei. Dann erfüllen die Stoffmengen yA und yB folgendes System von Differentialgleichungen:
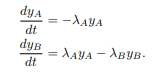
Bestimmen Sie die allgemeine Lösung dieses Systems bei vorgegebenen Anfangswerten von
yA(0) und yB(0) zum Zeitpunkt Null.
Hinweis: Die erste Gleichung des Systems ist entkoppelt, d.h. unabhängig von der zweiten.
Lösen Sie die erste Gleichung daher zuerst.
b) Bisher haben wir im Zerfallsgesetz die Zerfallsrate als Materialkonstante gesehen.
Es ist aber üblich, stattdessen die Halbwertszeit anzugeben. Das ist die Zeit, nach der die Hälfte der ursprünglichen Stoffmenge vorhanden ist, wenn das Nuklid nicht neu gebildet wird. Wie hängt die Halbwertszeit mit der Zerfallsrate zusammen? Welche Daten ergeben sich bei 241Pu und 241Am?