Zeigen Sie mit Hilfe des Mittelwertsatzes, dass |\tan (x)+\tan (y)| ≥|x+y| für alle x, y \in]-\frac{\pi}{2}, …

Question

Aufgabe:

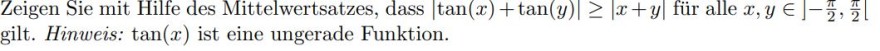
Text erkannt:

Zeigen Sie mit Hilfe des Mittelwertsatzes, dass \( |\tan (x)+\tan (y)| \geq|x+y| \) für alle \( x, y \in]-\frac{\pi}{2}, \frac{\pi}{2} \mid \) gilt. Hinweis: \( \tan (x) \) ist eine ungerade Funktion.

Problem/Ansatz:

Mein Problem ist, das ich nicht weiß wie ich das zeigen soll. Würde mich über jede Hilfe freuen.

Answer 1

Du brauchst hier nur einen kleine Vorzeichentrick. Außerdem ist die Ableitung \(\frac d{dt} \tan t = 1+\tan^2 t\) nützlich.

Per Mittelwertsatz (und Vorzeichentrick weil \(\tan\) ungerade) gilt

$$|\tan x + \tan y |= |\tan x - \tan (-y) | \stackrel{MWS}{=}\underbrace{(1+\tan^2 \xi)}_{\geq 1} \cdot |x -(-y)| = |x+y|$$