Berechne die Parallele p zu der Geraden f, die durch den Punkt Q(-7/-4) verläuft

Question

Aufgabe:

Berechne die Parallele p zu der Geraden f, die durch den Punkt Q(-7/-4) verläuft

Funktion F f(x)= -4/7( Bruch)•x+3

Answer 1

Die Steigung der gesuchten Geraden ist -4/7. Wenn die Steigung und ein Punkt gegeben sind, verwende ich die Punkt-Steigungs-Form - \( \frac{4}{7} \)=\( \frac{y+4}{x+7} \), Das kannst du nach y auflösen, um die übliche Form der Gleichung der Parallelen p zu bekommen.

Answer 2

Hallo und willkommen in der Mathelounge,

allgemeine Form einer Geraden: y = mx + n mit

m = Steigung, n = Schnittpunkt mit der y-Achse

Parallele Geraden haben die gleiche Steigung, also weißt du von der gesuchten Geraden

\(y=-\frac{4}{7}x+n\)

Um n zu bestimmen, setzt du die Koordinaten von Q in die Gleichung ein und löst nach n auf.

Gruß, Silvia

zum Vergleich:

[spoiler]

\(-4=-\frac{4}{7}\cdot (-7)+n\\ -4=4+n\\ -8=n\\ \)

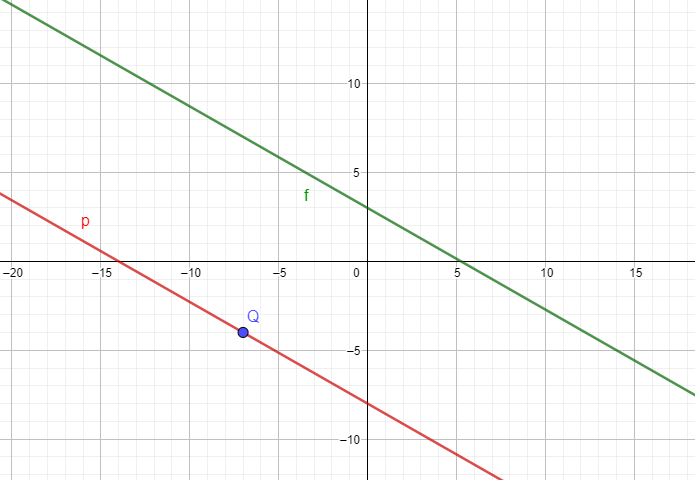
Damit lautet die Gleichung der gesuchten Geraden p

\(y=-\frac{4}{7}x-8\)

[/spoiler]

Answer 3

Es gibt so ein Ding namens Punktsteigungsform von Geraden. Du hast den Punkt (Q), und Du hast die Steigung (-4/7).

Answer 4

Punkt-Steigungs-Form

p(x) = m·(x - Px) + Py
p(x) = - 4/7·(x - (- 7)) + (- 4)
p(x) = - 4/7·(x + 7) - 4

Wenn man will, multipliziert man noch aus. Das aber nur um dem Lehrer zu zeigen das man es kann.

p(x) = - 4/7·x - 8