Jetzt sehe ich es!
Wir sehen nur das, was wir schon kennen. Wenn wir die chinesischen Schriftzeichen nicht kennen, sehen wir unten ein Zeichen, das für uns keine Bedeutung hat – außer vielleicht tj. Es ist das chinesische Schriftzeichen für die Silbe Li. Um die Bedeutung irgendeines Zeichens zu erkennen, muss dieses Zeichen samt Bedeutung in unserem Vorwissen abgespeichert sein.

Wir sehen nur das, was wir sehen wollen. Wer im untenstehenden Bild die Silhouette eines Pokals sehen will, wird sie sehen. Wer aber zwei Gesichter sehen will, die sich gegenseitig anschauen, wird auch diese sehen.

Was wir sehen wollen, kann auch von unserer aktuellen Disposition abhängen. Je nachdem ob man lieber an junge Mädchen denkt oder von alten Frauen umgeben ist, wird man das Mädchen oder die Greisin erkennen.

Auch in der Mathematik geht es darum, etwas zu sehen. Der Terminus, den manche Didaktiker für das Leitmotiv fast der gesamten Mathematik halten, heißt ‚Mustererkennung‘. Erkannte Muster korrespondieren immer mit Vorwissen, welches wiedererkannt wird. Welches Muster steckt in der Zahlenfolge 1, 8, 27, 64, 125, …? Nur wer die Kubikzahlen in seinem Vorwissen gespeichert hat, wird das Muster erkennen. Die Mustererkennung kann in diesem Falle für einige Menschen schwierig bis unmöglich sein. Betrachten wir eine weitere Zahlenfolge: 2, 5, 7, 10, 13, … . Nur die- oder derjenige, dem die ‚Upper Wythoff Sequence‘ schon einmal begegnet ist, kann das enthaltene Muster erkennen und vielleicht sogar mit einer mathematischen Formel beschreiben.
Ganz wichtig für die Mustererkennung ist unter Umständen der sogenannte ‚Repräsentationswechsel‘. Man betrachte dazu eine Punktmenge im Koordinatensystem.
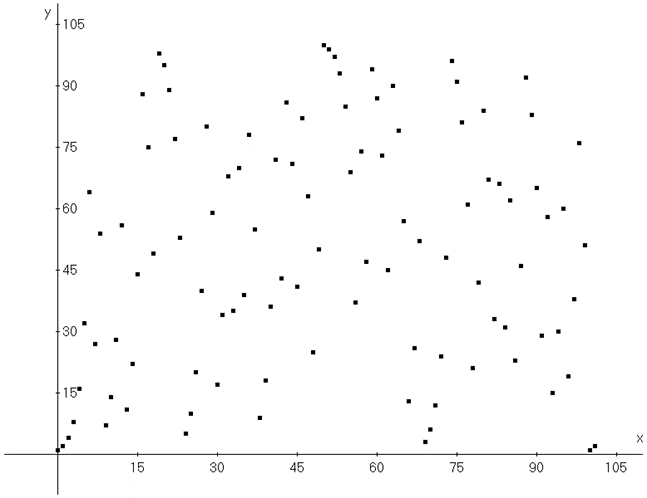
Man wird vermutlich kein Muster erkennen.
Die Wertetabelle zu diesem Muster ist eine andere Repräsentation desselben Musters und kann – bei umfangreichem Vorwissen – dazu beitragen, ein Muster zu erkennen. Man erkennt Teilsequenzen von Verdopplungen und weiß aus der Darstellung im Koordinatensystem, dass kein Funktionswert über 101 hinausgeht. Mit einiger Erfahrung kann man jetzt schließen, dass es sich um eine nach dem Modul 101 reduzierte Folge von Zweierpotenzen handelt.
Eine dritte Repräsentation derselben Zahlenfolge erhält man, wenn man den Zahlenstrahl auf einem Kreis mit 101 Teil-Strichen anordnet und jeweils eine Sehne von einem Folgenglied zum nächsten Folgenglied zieht.
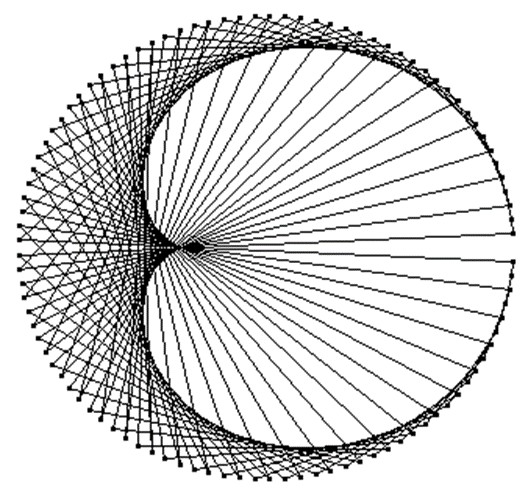
Damit gewinnt man zwar ein hübsches geometrisches Muster, dessen Beschreibung man allerdings auch nicht näherkommt, als mit Hilfe der Wertetabelle. Man könnte hier eine Nephroide erkennen, wie sie auf der Kaffeeoberfläche gesichtet wird, wenn im Winter früh am Morgen Licht in die Kaffeetasse fällt. Eine formale Musterbeschreibung wird vermutlich trotz dieser Erkenntnis nicht gelingen.
Es gibt Fälle, in denen man angesichts einer Darstellung autistisch reagiert und etwas, das man eigentlich kennt, nicht wiedererkennt. Das ist zum Beispiel der Fall, wenn man folgendes Bild zu ersten Mal sieht.

Nur ganz wenige Menschen erkennen hier das Bild einer Kuh. Wenn man allerdings einen Tipp bekommt, wird fast jede*r sagen: „Jetzt sehe ich es“.
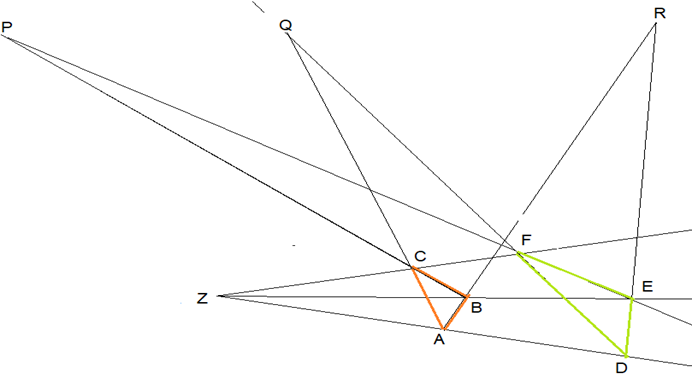
Ob ein Betrachter des untenstehenden Bildes den Satz von Desargues erkennt, hängt davon ab, ob er in der Lage ist, eine zweidimen-sionale Darstel-lung dreidimensional zu interpretieren. Dann schneiden sich die Ebenen, die durch A, B und C beziehungsweise durch D, E und F festgelegt sind in einer Geraden, auf der P, Q und R liegen. Hier geht es zwecks Repräsentationswechsel um einen Interpretationswechsel vom Zweidimensionale ins Dreidimensionale.
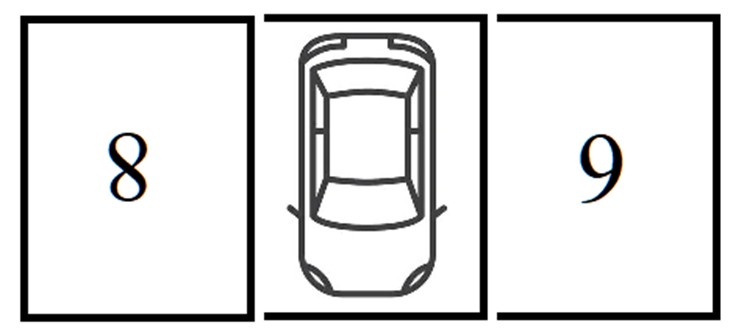
Und schließlich ist auch das Drehen eines Bildes ein Repräsentationswechsel. Im folgenden Bild führt eine Drehung um 180° dazu , die Frage zu beantworten. Welche Platznummer verdeckt das Auto?
Die oben herausgehobenen Termini ‚Mustererkennung‘ (einschließlich der formalen Musterbeschreibung) und ‚Repräsentationswechsel‘ (auch Interpretations- oder Perspektivwechsel) sind wichtige kognitive Handlungen, die jeder beherrschen sollte, der erfolgreich Mathematik betreiben will. Beide Handlungen setzen einen breiten Wissens- und Erfahrungsfundus voraus.
