Lässt sich die Abschätzung dann einfach mit dem Lim gegen unendlich berechnen und das daraus resultierende Ergebniss …

Question

Aufgabe:

Text erkannt:

1. Untersuchen Sie die folgenden Reihen auf Konvergenz.
a) \( \sum \limits_{n=1}^{\infty} \frac{n+2}{n^{3}+\sin (n)+1} \)
b) \( \sum \limits_{n=2}^{\infty} \frac{n^{2}-3}{n^{3}+\sin (n)+1} \)

Problem/Ansatz:

Ansatz Aufgabe a)

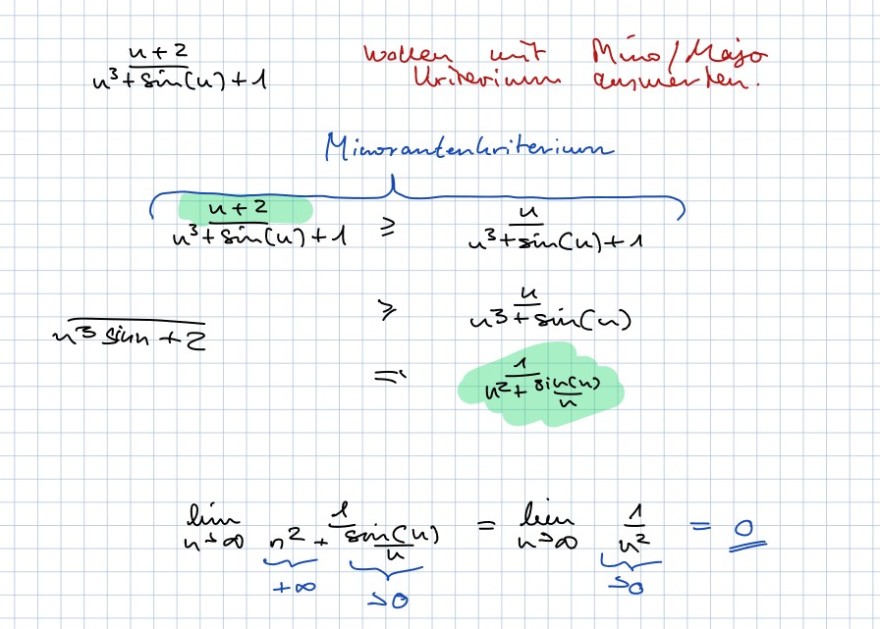
Text erkannt:

\( \frac{u+2}{u^{3}+\sin (u)+1} \)
wallen wit Mino/Majo
Urinerimm auswerten.
Miworantenhriterium
\( u^{3} \frac{u+2}{\sin (u)+1 \geqslant} \frac{u}{u^{3}+\sin (u)+1} \)
\( \frac{n^{3} \sin n+2}{n^{3}+\sin (n)} \)
\( \Rightarrow \quad \frac{1}{u^{2}+\frac{8 i n}{n}(n)} \)

Ansatz Aufgabe b)

Text erkannt:

b) \( \sum \limits_{n=2}^{\infty} \frac{u^{2}-3}{n^{3}+\sin (u)+1} \leq \frac{u^{2}}{u^{3}+\sin (u)} \)
Mojoranten Ceriterium
\( \begin{array}{l} \lim \limits_{n \rightarrow \infty} \underbrace{\frac{u^{2}}{n^{2}}}_{x^{2}\left(n+\frac{x^{2}}{u^{3}+\sin (n)}(n)\right.} \\ u+\frac{1}{\sqrt[3]{n} \frac{n n}{n^{2}}} \\ \end{array} \)

ich und mein Kollege sind uns, wie so oft, unstimmig. Bei der Konvergenzbetrachtung haben wir uns mit dem Majo/Mino-Kriterium auseinander gesetzt und sowohl die a) als auch die b) nach oben/unten abgeschätzt. Auch hier sind wir uns noch nicht ganz Sicher.

Grundsätzlich sind wir uns unstimmig, wie es nach der Abschätzung weitergeht. Kann direkt die Betrachtung gegen unendlich gemacht werden, wird diese so überhaupt gemacht da es ja im umkehrschluss eigentlich die Grenzwertbetrachtung ist.

Lässt sich die Abschätzung dann einfach mit dem Lim gegen unendlich berechnen und das daraus resultierende Ergebniss ist meine Lösung?

Beste Grüße

Answer 1

(0)  Es ist \(0\le1+\sin(n)\le2\) für alle \(n\in\N\).

(1)  Für alle \(n\ge1\) gilt$$0\le\frac{n+2}{n^3+\sin(n)+1}\le\frac{n+2n}{n^3+0}=\frac{3n}{n^3}=\frac3{n^2}.$$Daraus folgt Konvergenz nach dem Majorantenkriterium.

(2)  Für alle \(n\ge3\) gilt$$\frac{n^2-3}{n^3+\sin(n)+1}\ge\frac{n^2-3}{n^3+2}\ge\frac{n^2-3}{n^3+2n^3}=\frac{n^2-3}{3n^3}=\frac{2n^2-6}{6n^3}=\frac{n^2+(n^2-6)}{6n^3}\ge\frac{n^2}{6n^3}=\frac1{6n}.$$Daraus folgt Divergenz nach dem Minorantenkriterium.