Maximal zulässige Schachtgröße

Question

Aufgabe:

Hallo Zusammen,

das Rechteck hat folgende Maße breite=8 mm und Länge=250mm es soll entlang eines schachtes Transportiert werden ohne mit den vorhergegangenen Rechteck (selbe maße) sich zu verklemmen. Also die maximal zulässige Schachtgröße Kmax ist gesucht.

Problem/Ansatz:

Comments

Liegt das andere Recheck genauso schief drin? Die Augabenformulierung ist unzureichend.

Die kommen aneinander vorbei, wenn Kmax=2*8mm ist. aber das war sicher nicht gefragt.

---

Ja das Rechteck soll anscheinend in dieser Position verbleiben und auch so Transportiert werden. Als Tipp sollte man die Untere Rechteckfläche betrachten. Als lösung ergibt sich ein Wert von 15,992.

---

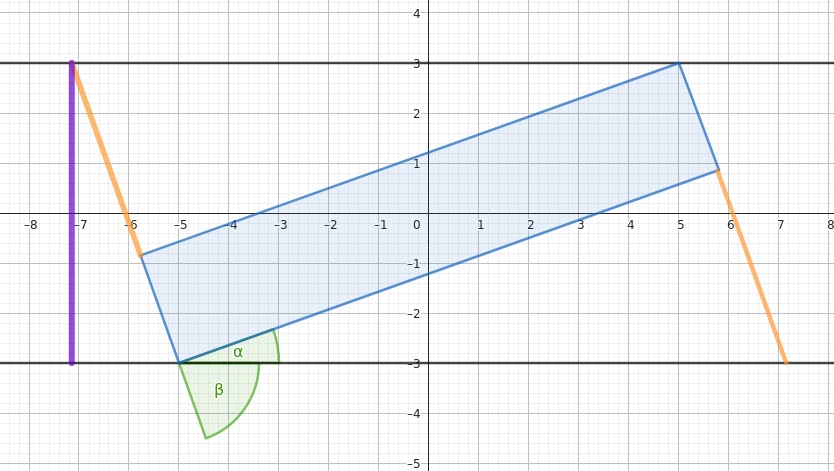
Nenne orangene Strecken y und lila Strecke k

$$ \alpha =\arctan\left( \frac{y}{250} \right) $$ $$ \sin(\beta) = \frac{k}{y+8} $$

(Gegenwinkel betrachten). Mit \( \alpha + \beta = \frac{\pi}{2} \) erhält man

$$ k = (y+8) \sin\left(\frac{\pi}{2} - \arctan\left( \frac{y}{250} \right)\right) $$

Das kann man jetzt noch bisschen vereinfachen und dann im Intervall \( 0 \le y \le 8 \) maximieren. (Wenn y < 0 ist der Schacht für das Bauteil zu schmal und für y > 8 kann es sich verklemmen) Ergebnis:

$$ \frac{2000}{\sqrt{15641}} \approx 15.992 $$

Answer 1

Blauer Winkel: tan α = 8/250  

α = 1,83°

Rote Strecke: 2*8 mm = 16 mm

grüne Strecke: 16 mm * cos 1,83° =15,99 mm.

Spaltbreite 15,99 mm + 8 mm = 23,99 mm.

Comments

danke vielmals