Aufgabe: Der einarmige Bandit kann in jedem der vier Fenster eine der Ziffern 1, 2 oder 3 ausgeben.
a) Wie viele verschiedene Ergebnisse gibt es insgesamt?
b) Bestimmen Sie die Wahrscheinlichkeit des Ereignisses:
A: Es erscheint die Ziffernfolge 1 2 3 3. (erledigt)
B: Es erscheint genau zweimal die Ziffer 1. (erledigt)
C: Es erscheinen nur Einsen.(erledigt)
D: Es erscheinen nur gleiche Ziffern. (erledigt)
2 1 2 3 sas.
c) Das Gerät wird 10-mal bedient. Mit welcher Wahrscheinlichkeit tritt das Ereignis B nicht ein einziges Mal ein? Mit welcher Wahrscheinlichkeit tritt es genau 2-mal ein?
d) Wie oft muss man das Gerät mindestens in Gang setzen, damit mit einer Wahrscheinlichke von wenigstens 95% mindestens einmal das Ereignis B eintritt?
e) Bei einem Einsatz von 1 € pro Spiel gewinnt man 30 €, wenn die Ziffernfolge 3333 komm und 5 €, wenn die Ziffernfolge 2 ××2 kommt, also 2112 oder 2222 oder 2332. Lohnt sich der Spiel für den Spieler? Wie viel Gewinn/Verlust ist für den Betreiber an einem Tag mit 8 Stun den zu erwarten, wenn pro Stunde ca. 20 Spiele stattfinden?
f) Johannes berichtet, dass er gerade fünfmal hintereinander gewonnen hat (Ziffernfolge 333.
oder 2 xx2). Beurteilen Sie diese Aussage bezüglich ihrer Glaubwürdigkeit.
Jana sagt, dass sie bei 100 Spielen ca. 20- bis 30-mal das Ereignis B beobachtet hat. Ist di glaubhaft? (Verwenden Sie bei der Lösung dieser Aufgabe für die Wahrscheinlichkeit de
Ereignisses B den Näherungswert 0,3).
Problem/Ansatz: Könnte vielleicht bitte jemand meine Hausaufgaben kontrollieren. Ich bin mir leider nicht genau sicher, wie ich bei d) und e) vorgehen soll
Habe es trotzdem mal versucht oder meine Ideen hingeschrieben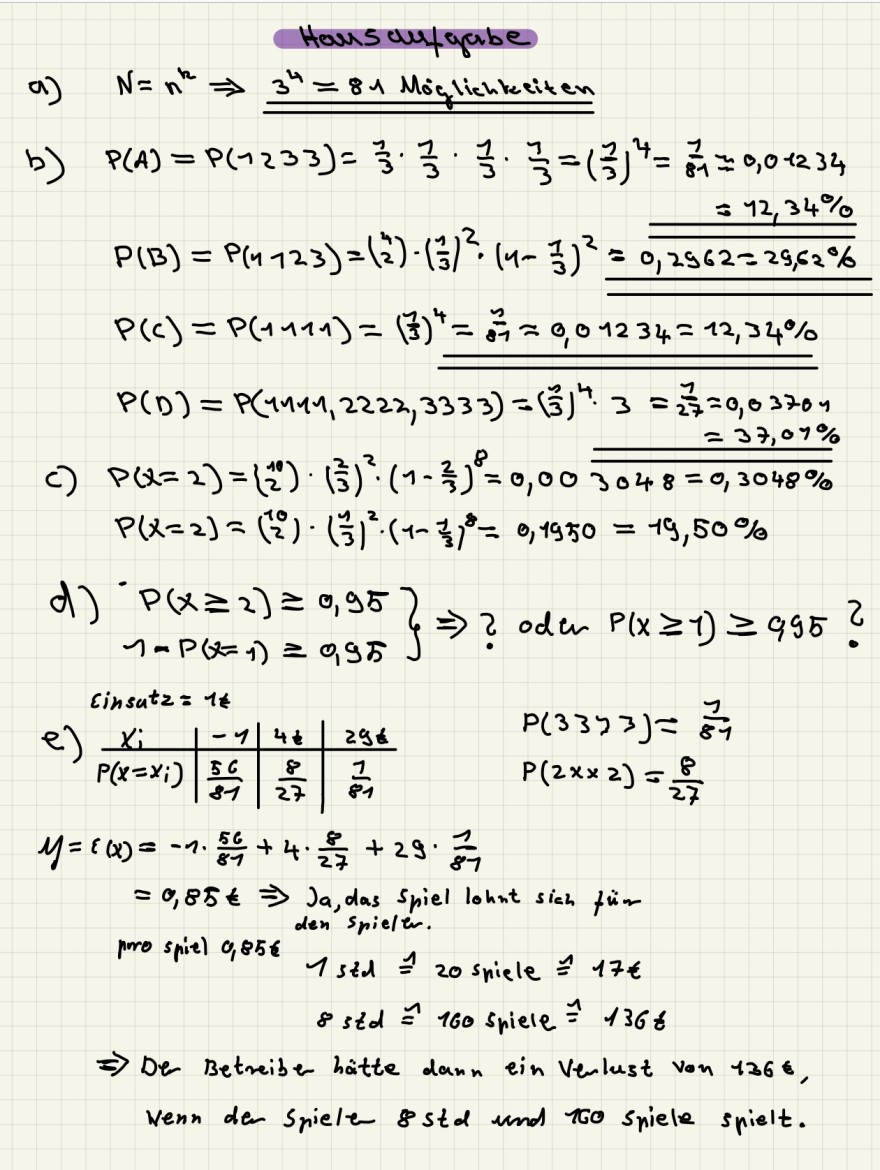
Text erkannt:
Hous curfarabe
a) \( N=n^{2} \Rightarrow 3^{4}=81 \) Mojglichleeiten
\( \begin{array}{l} \text { b) } P(A)=P(1233)=\frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3}=\left(\frac{1}{3}\right)^{4}=\frac{1}{81}=0,01234 \\ P(B)=P(4723)=\left(\begin{array}{l} 4 \\ 2 \end{array}\right) \cdot\left(\frac{1}{3}\right)^{2} \cdot\left(4-\frac{1}{3}\right)^{2}=\frac{=12,34 \%}{0,2962=29,62 \%} \\ P(c)=P(1111)=\left(\frac{1}{3}\right)^{4}=\frac{2}{81}=0,01234=12,34 \% \\ P(D)=P(4411,2222,3333)=\left(\frac{1}{3}\right)^{4} \cdot 3=\frac{1}{27}=0,03704 \\ =37,07 \% \\ \end{array} \)
\( \text { C) } \begin{aligned} P(x=2) & =\left(\begin{array}{c} 10 \\ 2 \end{array}\right) \cdot\left(\frac{2}{3}\right)^{2} \cdot\left(1-\frac{2}{3}\right)^{8}=0,00 \overline{3048=0,3048 \%} \\ P(x=2) & =\left(\begin{array}{c} 10 \\ 2 \end{array}\right) \cdot\left(\frac{1}{3}\right)^{2} \cdot\left(1-\frac{1}{3}\right)^{8}=0,1950=19,50 \% \end{aligned} \)
\( \text { d) } \left.\begin{array}{l} P(x \geq 2) \geq 0,95 \\ 1-P(x=1) \geq 0,95 \end{array}\right\} \Rightarrow 2 \text { oder } P(x \geq 1) \geq 9,95 ? \)
\( \begin{array}{l} \text { cinsutz }=1 \mathrm{t} \\ \text { e) } \begin{array}{l|l|l|ll} x_{i} & -1 & 4 t & 296 & P(33 y 3)=\frac{1}{81} \\ \hline P\left(x=x_{i}\right) & \frac{56}{81} & \frac{8}{27} & \frac{1}{81} & P(2 x \times 2)=\frac{8}{27} \end{array} \\ y=\varepsilon(x)=-1 \cdot \frac{56}{81}+4 \cdot \frac{8}{27}+29 \cdot \frac{1}{87} \\ =0,85 t \Rightarrow \text { Ja, das spiel lohnt sich fuir } \\ \end{array} \)
\( \Rightarrow \) Der Betreiber hatte dann ein verlust von 1366, Wenn den Spiele 8 std und 100 sriele spielt.
Text erkannt:
Hous curfarabe
a) \( N=n^{2} \Rightarrow 3^{4}=81 \) Mojglichleeiten
\( \begin{array}{l} \text { b) } P(A)=P(1233)=\frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3}=\left(\frac{1}{3}\right)^{4}=\frac{1}{81}=0,01234 \\ P(B)=P(4723)=\left(\begin{array}{l} 4 \\ 2 \end{array}\right) \cdot\left(\frac{1}{3}\right)^{2} \cdot\left(4-\frac{1}{3}\right)^{2}=\frac{=12,34 \%}{0,2962=29,62 \%} \\ P(c)=P(1111)=\left(\frac{1}{3}\right)^{4}=\frac{2}{81}=0,01234=12,34 \% \\ P(D)=P(4411,2222,3333)=\left(\frac{1}{3}\right)^{4} \cdot 3=\frac{1}{27}=0,03704 \\ =37,07 \% \\ \end{array} \)
\( \text { C) } \begin{aligned} P(x=2) & =\left(\begin{array}{c} 10 \\ 2 \end{array}\right) \cdot\left(\frac{2}{3}\right)^{2} \cdot\left(1-\frac{2}{3}\right)^{8}=0,00 \overline{3048=0,3048 \%} \\ P(x=2) & =\left(\begin{array}{c} 10 \\ 2 \end{array}\right) \cdot\left(\frac{1}{3}\right)^{2} \cdot\left(1-\frac{1}{3}\right)^{8}=0,1950=19,50 \% \end{aligned} \)
\( \text { d) } \left.\begin{array}{l} P(x \geq 2) \geq 0,95 \\ 1-P(x=1) \geq 0,95 \end{array}\right\} \Rightarrow 2 \text { oder } P(x \geq 1) \geq 9,95 ? \)
\( \begin{array}{l} \text { cinsutz }=1 \mathrm{t} \\ \text { e) } \begin{array}{l|l|l|ll} x_{i} & -1 & 4 t & 296 & P(33 y 3)=\frac{1}{81} \\ \hline P\left(x=x_{i}\right) & \frac{56}{81} & \frac{8}{27} & \frac{1}{81} & P(2 x \times 2)=\frac{8}{27} \end{array} \\ y=\varepsilon(x)=-1 \cdot \frac{56}{81}+4 \cdot \frac{8}{27}+29 \cdot \frac{1}{87} \\ =0,85 t \Rightarrow \text { Ja, das spiel lohnt sich fuir } \\ \end{array} \)
\( \Rightarrow \) Der Betreiber hatte dann ein verlust von 1366, Wenn den Spiele 8 std und 100 sriele spielt.